练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在正方形网格中，网格线的交点称为格点，如图是 3×3 的正方形网格，已知 A，B 是两格点，C是不同于点A和B的格点，下列说法正确的是（ ）.

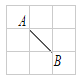
    A.ΔABC是直角三角形，这样的点C有4个

    B.ΔABC是等腰三角形，这样的点C有4个

    C.ΔABC是等腰直角三角形，这样的点C有6个

    D.ΔABC是等腰直角三角形，这样的点C有2个

    【答案】C

    【解析】

    运用分类讨论思想，分别画出满足ΔABC是等腰三角形和ΔABC是等腰直角三角形的点，则问题可解.

    解：当ΔABC是等腰直角三角形时，如图：

    分情况讨论①AB为等腰直角△ABC底边时，符合条件的C点有2个；
    ②AB为等腰直角△ABC其中的一条腰时，符合条件的C点有4个．
    故构成等腰直角三角形的点一共有6个．故ΔABC是直角三角形的点也有6个.

    当ΔABC是等腰三角形时，如图

    ，

    分情况讨论①AB为等腰△ABC的底边时，符合条件的C点有4个；
    ②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．
    故构成等腰三角形的点一共有8个．

    故应选C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解方程：(1)2x2－x－2=0（配方法） (2)5－4x－12＝0（用求根公式）

    （3） （4）2（x－3）2 =x（x－3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线y=与x轴、y轴分别交于A、B两点，P是以C（0，2）为圆心，2为半径的圆上一动点，连结PA、PB．则△PAB面积的最小值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=5，AD=a（a＞5）.点P在以A为圆心、AB长为半径的⊙A上，且在矩形ABCD的内部，P到AD、CD的距离PE、PF相等.

    （1）若a =7，求AE长；

    （2）若⊙A上满足条件的点P只有一个，求a的值；

    （3）若⊙A上满足条件的点P有两个，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC是等边三角形.

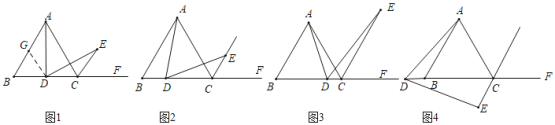
    (1)如图1，点D是边BC的中点，∠ADE＝60°，且DE交△ABC外角∠ACF的平分线CE于点E，求证：AD＝DE；(提示：取AB的中点G，连接DG)

    (2)小颖对(1)题进行了探索：如果将(1)题中的“点D是边BC的中点”改为“点D是直线BC上任意一点(B、C两点除外)”，其它条件不变，结论AD＝DE是否仍然成立？小颖将点D的位置分为三种情形，画出了图2、图3、图4，现在请你在图2、图3、图4中选择一种情形，帮小颖验证：结论AD＝DE是否仍然成立？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在2014年“元旦”前夕，某商场试销一种成本为30元的文化衫，经试销发现，若每件按34元的价格销售，每天能卖出36件；若每件按39元的价格销售，每天能卖出21件．假定每天销售件数y（件）是销售价格x(元)的一次函数．

    （1）直接写出y与x之间的函数关系式.

    （2）在不积压且不考虑其他因素的情况下，每件的销售价格定为多少元时，才能使每天获得的利润P最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了实现“畅通市区”的目标，市地铁一号线准备动工，市政府现对地铁一号线第标段工程进行招标，施工距离全长为米．经招标协定，该工程由甲、乙两公司承建，甲、乙两公司施工方案及报价分别为：

    甲公司施工单价（万元/米）与施工长度（米）之间的函数关系为，

    乙公司施工单价（万元/米）与施工长度（米）之间的函数关系为．

    （注：工程款施工单价施工长度）

    如果不考虑其他因素，单独由甲公司施工，那么完成此项工程需工程款多少万元？

    考虑到设备和技术等因素，甲公司必须邀请乙公司联合施工，共同完成该工程．因设备共享，两公司联合施工时市政府可节省工程款万元（从工程款中扣除）．

    ①如果设甲公司施工米，那么乙公司施工________米，其施工单价________万元/米，试求市政府共支付工程款（万元）与（米）之间的函数关系式；

    ②如果市政府支付的工程款为万元，那么应将多长的施工距离安排给乙公司施工？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c的图象如图所示，下列结论正确的是（　　）

    ①b＜1；②2a+b＞0；③a+c+1＞0；④a﹣b+c＜0；⑤最大值为3．

    A. ②③④⑤ B. ②③④ C. ②③ D. ①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某文具店销售一种进价为每本10元的笔记本，为获得高利润，以不低于进价进行销售，结果发现，每月销售量y与销售单价x之间的关系可以近似地看作一次函数：y=﹣5x+150，物价部门规定这种笔记本每本的销售单价不得高于18元．

    （1）当每月销售量为70本时，获得的利润为多少元；

    （2）该文具店这种笔记本每月获得利润为W元，求每月获得的利润W元与销售单价x之间的函数关系式，并写出自变量的取值范围；

    （3）当销售单价定为多少元时，每月可获得最大利润，最大利润为多少元？

    查看答案和解析>>

    同步练习册答案