
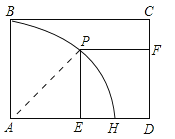
【题目】如图,在矩形ABCD中,AB=5,AD=a(a>5).点P在以A为圆心、AB长为半径的⊙A上,且在矩形ABCD的内部,P到AD、CD的距离PE、PF相等.
(1)若a =7,求AE长;
(2)若⊙A上满足条件的点P只有一个,求a的值;
(3)若⊙A上满足条件的点P有两个,求a的取值范围.

【答案】(1)3或4 ;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接AP,根据勾股定理解答即可;
(2)设AE=x,则(a﹣x)2+x2=25有两个相等的实数根,由根的判别式解答即可;
(3)设AE=x,则(a﹣x)2+x2=25有两个不相等的实数根,由根的判别式解答即可.
(1)连接AP.设AE=x,则(7﹣x)2+x2=25,解得:x=3或4.
所以AE的长为3或4;
(2)设AE=x,则(a﹣x)2+x2=25有两个相等的实数根,∴方程![]() 的判别式△=0,∴
的判别式△=0,∴![]() ,解得:a=
,解得:a=![]() .
.
∵a>0,∴a=![]() .
.
(3)设AE=x,则(a﹣x)2+x2=25有两个不相等的实数根,∴方程![]() 的判别式△>0,∴
的判别式△>0,∴![]() ,解得:a>
,解得:a>![]() 或a<
或a<![]() .
.
∵a>5,∴5<a<5![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】标有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为
六个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为![]() ,朝下一面的数为
,朝下一面的数为![]() ,得到平面直角坐标系中的一个点
,得到平面直角坐标系中的一个点![]() .已知小华前二次掷得的两个点所确定的直线经过点
.已知小华前二次掷得的两个点所确定的直线经过点![]() ,则他第三次掷得的点也在这条直线上的概率为________.
,则他第三次掷得的点也在这条直线上的概率为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划召开“诚信在我心中”主题教育活动,需要选拔活动主持人,经过全校学生投票推荐,有2名男生和1名女生被推荐为候选主持人.
(1)小明认为,如果从3名候选主持人中随机选拔1名,不是男生就是女生,因此选出的主持人是男生和女生的可能性相同,你同意他的说法吗?为什么?
(2)如果从3名候选主持人中随机选拔2名,请通过列表或画树状图求选拔的2名主持人恰好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助贫困家庭脱困,精准扶贫小组帮助一农户建立如图所示的长方形养鸡场,长方形的面积为45m2(分为两片),养鸡场的一边靠着一面长为14m的墙,另几条边用总长为22m的竹篱笆围成,每片养鸡场的前面各开一个宽1m的门.求这个养鸡场的长与宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.
计算:(1)i.i2.i3.i4
(2)i+i2+i3+i4+…+i2017+i2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,网格线的交点称为格点,如图是 3×3 的正方形网格,已知 A,B 是两格点,C是不同于点A和B的格点,下列说法正确的是( ).
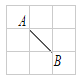
A.ΔABC是直角三角形,这样的点C有4个
B.ΔABC是等腰三角形,这样的点C有4个
C.ΔABC是等腰直角三角形,这样的点C有6个
D.ΔABC是等腰直角三角形,这样的点C有2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,F是AD中点,延长BC到E,CE=![]() BC,连结DE、CF,∠B=60°,AB=3,AD=4,则DE=_______________
BC,连结DE、CF,∠B=60°,AB=3,AD=4,则DE=_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com