
【题目】如图,在平行四边形ABCD中,F是AD中点,延长BC到E,CE=![]() BC,连结DE、CF,∠B=60°,AB=3,AD=4,则DE=_______________
BC,连结DE、CF,∠B=60°,AB=3,AD=4,则DE=_______________

【答案】![]()
【解析】
先证明四边形CEDF是平行四边形,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
又∵F是AD的中点,
∴FD=![]() AD.
AD.
∵CE=![]() BC,
BC,
∴FD=CE.
又∵FD∥CE,
∴四边形CEDF是平行四边形,
∴DE=CF.
过D作DG⊥CE于点G,如图,
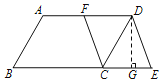
∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=3,BC=AD=4.
∴∠DCE=∠B=60°.
在Rt△CDG中,∠DGC=90°,
∴∠CDG=30°,
∴CG=![]() CD=
CD=![]() .
.
由勾股定理,得DG=![]() .
.
∵CE=![]() BC=2,
BC=2,
∴GE=![]() .
.
在Rt△DEG中,∠DGE=90°,
∴DE=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=a(a>5).点P在以A为圆心、AB长为半径的⊙A上,且在矩形ABCD的内部,P到AD、CD的距离PE、PF相等.
(1)若a =7,求AE长;
(2)若⊙A上满足条件的点P只有一个,求a的值;
(3)若⊙A上满足条件的点P有两个,求a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x(元)的一次函数.
(1)直接写出y与x之间的函数关系式.
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了实现“畅通市区”的目标,市地铁一号线准备动工,市政府现对地铁一号线第![]() 标段工程进行招标,施工距离全长为
标段工程进行招标,施工距离全长为![]() 米.经招标协定,该工程由甲、乙两公司承建,甲、乙两公司施工方案及报价分别为:
米.经招标协定,该工程由甲、乙两公司承建,甲、乙两公司施工方案及报价分别为:
![]() 甲公司施工单价
甲公司施工单价![]() (万元/米)与施工长度
(万元/米)与施工长度![]() (米)之间的函数关系为
(米)之间的函数关系为![]() ,
,
![]() 乙公司施工单价
乙公司施工单价![]() (万元/米)与施工长度
(万元/米)与施工长度![]() (米)之间的函数关系为
(米)之间的函数关系为![]() .
.
(注:工程款![]() 施工单价
施工单价![]() 施工长度)
施工长度)
![]() 如果不考虑其他因素,单独由甲公司施工,那么完成此项工程需工程款多少万元?
如果不考虑其他因素,单独由甲公司施工,那么完成此项工程需工程款多少万元?
![]() 考虑到设备和技术等因素,甲公司必须邀请乙公司联合施工,共同完成该工程.因设备共享,两公司联合施工时市政府可节省工程款
考虑到设备和技术等因素,甲公司必须邀请乙公司联合施工,共同完成该工程.因设备共享,两公司联合施工时市政府可节省工程款![]() 万元(从工程款中扣除).
万元(从工程款中扣除).
①如果设甲公司施工![]() 米
米![]() ,那么乙公司施工________米,其施工单价
,那么乙公司施工________米,其施工单价![]() ________万元/米,试求市政府共支付工程款
________万元/米,试求市政府共支付工程款![]() (万元)与
(万元)与![]() (米)之间的函数关系式;
(米)之间的函数关系式;
②如果市政府支付的工程款为![]() 万元,那么应将多长的施工距离安排给乙公司施工?
万元,那么应将多长的施工距离安排给乙公司施工?
查看答案和解析>>
科目:初中数学 来源: 题型:
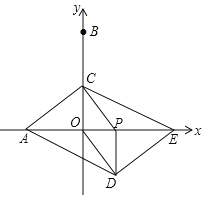
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
(1)当点C运动到线段OB的中点时,求t的值及点E的坐标.
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,下列结论正确的是( )
①b<1;②2a+b>0;③a+c+1>0;④a﹣b+c<0;⑤![]() 最大值为3.
最大值为3.

A. ②③④⑤ B. ②③④ C. ②③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.

(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com