
����Ŀ��Ϊ��ʵ������ͨ��������Ŀ�꣬�е���һ�������������������ֶԵ���һ���ߵ�![]() ��ι��̽����б꣬ʩ������ȫ��Ϊ
��ι��̽����б꣬ʩ������ȫ��Ϊ![]() �ף����б�Э�����ù����ɼס�������˾�н����ס�������˾ʩ�����������۷ֱ�Ϊ��
�ף����б�Э�����ù����ɼס�������˾�н����ס�������˾ʩ�����������۷ֱ�Ϊ��
![]() ��˾ʩ������
��˾ʩ������![]() ����Ԫ/�ף���ʩ������
����Ԫ/�ף���ʩ������![]() ���ף�֮��ĺ�����ϵΪ
���ף�֮��ĺ�����ϵΪ![]() ��
��
![]() �ҹ�˾ʩ������
�ҹ�˾ʩ������![]() ����Ԫ/�ף���ʩ������
����Ԫ/�ף���ʩ������![]() ���ף�֮��ĺ�����ϵΪ
���ף�֮��ĺ�����ϵΪ![]() ��
��
��ע�����̿�![]() ʩ������
ʩ������![]() ʩ�����ȣ�
ʩ�����ȣ�
![]() ����������������أ������ɼ�˾ʩ������ô��ɴ�����蹤�̿������Ԫ��
����������������أ������ɼ�˾ʩ������ô��ɴ�����蹤�̿������Ԫ��
![]() ���ǵ��豸�ͼ��������أ���˾���������ҹ�˾����ʩ������ͬ��ɸù��̣����豸����������˾����ʩ��ʱ�������ɽ�ʡ���̿�
���ǵ��豸�ͼ��������أ���˾���������ҹ�˾����ʩ������ͬ��ɸù��̣����豸����������˾����ʩ��ʱ�������ɽ�ʡ���̿�![]() ��Ԫ���ӹ��̿��п۳�����
��Ԫ���ӹ��̿��п۳�����
��������˾ʩ��![]() ��
��![]() ����ô�ҹ�˾ʩ��________�ף���ʩ������
����ô�ҹ�˾ʩ��________�ף���ʩ������![]() ________��Ԫ/�ף�������������֧�����̿�
________��Ԫ/�ף�������������֧�����̿�![]() ����Ԫ����
����Ԫ����![]() ���ף�֮��ĺ�����ϵʽ��
���ף�֮��ĺ�����ϵʽ��
�����������֧���Ĺ��̿�Ϊ![]() ��Ԫ����ôӦ�����ʩ�����밲�Ÿ��ҹ�˾ʩ����
��Ԫ����ôӦ�����ʩ�����밲�Ÿ��ҹ�˾ʩ����
���𰸡�(300a),(0.05a+0.8). Ӧ��200��100�׳���ʩ�����밲�Ÿ��ҹ�˾ʩ��.
��������
��1����x=300����y1����ʽ�м�����ֵ��
��2��������֧���Ĺ��̿�=��˾���ù��̿�+�ҹ�˾���ù��̿�-��ʡ���̿�140���ֱ��ʾ������˾���ù��̿���ɵ�P�ı���ʽ��
��3����P=2900ʱ����a�ķ��̣����a��ֵ������300-a��ý��ۣ�
(1)������ã�(27.80.09��300)��300=240(��Ԫ).
�𣺼�˾������ɴ�����蹤�̿�240��Ԫ��
(2)��(300a),(0.05a+0.8).
������,��P=(27.80.09a)a+(0.05a+0.8)(300a)140=27.8a0.09a20.05a2+14.2a+100=0.14a2+42a+100��
����P=2900ʱ,0.14a2+42a+100=2900��
����,�ã�a2300a+20000=0��
��ã�a1=100,a2=200��
��300a=200��300a=100.
��Ӧ��200��100�׳���ʩ�����밲�Ÿ��ҹ�˾ʩ����
�ʴ�Ϊ(300a),(0.05a+0.8).


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
��![]() ��
��![]() ����������
����������![]() ����������ͬ�Ľ��㣬������������֮��ľ���С��
����������ͬ�Ľ��㣬������������֮��ľ���С��![]() �������н��ۣ�
�������н��ۣ�
��![]() ����
����![]() ����
����![]() ����
����![]() �����н�����ȷ���ǣ� ��
�����н�����ȷ���ǣ� ��
A. �٢� B. �ڢۢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����һԪ���η���x2=��1û��ʵ��������������һ��ʵ����ƽ�����ک�1�������ǹ涨һ��������i����ʹ������i2=��1��������x2=��1��һ����Ϊi�������ҽ�һ���涨��һ��ʵ�����������������������㣬��ԭ�������ɺ����㷨����Ȼ������������i1��i��i2����1��i3��i2i����i��i4����i2��2������1��2=1���Ӷ���������������n�����ǿ��Եõ�i4n+1��i4ni��i��ͬ���ɵ�i4n+2����1��i4n+3����i��i4n��1��
���㣺��1��i��i2��i3��i4
��2��i+i2+i3+i4+��+i2017+i2018��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У������ߵĽ����Ϊ��㣬��ͼ�� 3��3 ��������������֪ A��B ������㣬C�Dz�ͬ�ڵ�A��B�ĸ�㣬����˵����ȷ���ǣ� ��.
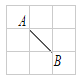
A.��ABC��ֱ�������Σ������ĵ�C��4��
B.��ABC�ǵ��������Σ������ĵ�C��4��
C.��ABC�ǵ���ֱ�������Σ������ĵ�C��6��
D.��ABC�ǵ���ֱ�������Σ������ĵ�C��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������й���һ��![]() Ԫ/ǧ�˵���ɫʳƷ�������
Ԫ/ǧ�˵���ɫʳƷ�������![]() Ԫ/ǧ�����ۣ���ôÿ����۳�
Ԫ/ǧ�����ۣ���ôÿ����۳�![]() ǧ�ˣ������۾���֪��ÿ��������
ǧ�ˣ������۾���֪��ÿ��������![]() ��ǧ�ˣ������۵���
��ǧ�ˣ������۵���![]() ��Ԫ��
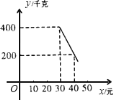
��Ԫ��![]() ��������ͼ��ʾ��һ�κ�����ϵ��
��������ͼ��ʾ��һ�κ�����ϵ��
![]() �����
�����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
![]() �����������������۸���ɫʳƷÿ��������Ϊ
�����������������۸���ɫʳƷÿ��������Ϊ![]() Ԫ�������۵���Ϊ��ֵʱ��ÿ��ɻ�����������������Ƕ��٣�
Ԫ�������۵���Ϊ��ֵʱ��ÿ��ɻ�����������������Ƕ��٣�
![]() �����г����飬����ɫʳƷÿ��ɻ�������
�����г����飬����ɫʳƷÿ��ɻ�������![]() Ԫ���ָó��о���Ҫ��ÿ�����õ���
Ԫ���ָó��о���Ҫ��ÿ�����õ���![]() Ԫ����������ó���ȷ����ɫʳƷ���۵���
Ԫ����������ó���ȷ����ɫʳƷ���۵���![]() �ķ�Χ��ֱ��д������
�ķ�Χ��ֱ��д������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�F��AD�е㣬�ӳ�BC��E��CE=![]() BC������DE��CF����B=60�㣬AB=3��AD=4����DE=_______________
BC������DE��CF����B=60�㣬AB=3��AD=4����DE=_______________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��������������������y=ax2+bx+l��x����������ͬ�Ľ���A��B����A��B��ԭ��ľ��붼С��1����a+b����Сֵ���ڣ�������
A. 16 B. 10 C. 4 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������Rt��ABC������Rt��ADE��AB��AC��AD��AE��AB��AC��AD��AE��CD��AE��BE�ֱ��ڵ�M��F��

��1����֤����DAC�ա�EAB.
��2����֤��CD��BE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D=��C=90����E��DC���е㣬AEƽ����DAB����DEA=28��������ABE�Ķ�����__________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com