
����Ŀ����֪���κ���y=x2��2x��3
��1���������֪�Ķ��κ�������y=��x��h��2+k����ʽ������ƽ��ֱ������ϵ�л�������ͼ��
��2�����A��x1��y1����B��x2��y2���ǣ�1�������ϵ����㣬��x1��x2��1����ֱ��д��y1��y2�Ĵ�С��ϵΪ�� ����
��3�����ã�1���е�ͼ���ʾ������x2��2x��1=0�ĸ������ڣ�1����ͼ���ϼ��ɣ�Ҫ������ͼ�ۼ���

���𰸡���1����ͼ����������2��y1��y2����3����ͼ��x1��x2Ϊ����x2��2x��1=0��������
��������
��1���Ȱѽ���ʽ��ɶ���ʽ�õ������ߵĶ�������Ϊ��1��-4�����������������y��Ľ����������������x��Ľ������꣬Ȼ��������㷨�������κ���ͼ����
��2�����ö��κ��������ʽ�����⣻
��3����ֱ��y=-2�������ߵĽ��㣬��������ĺ�����Ϊ����x2-2x-1=0��������
��1��y=x2��2x��3=��x��1��2��4��
�����ߵĶ�������Ϊ��1����4����
��x=0ʱ��y=x2��2x��3=��3������������y��Ľ�������Ϊ��0����3����
��y=0ʱ��x2��2x��3=0�����x1=��1��x2=3����������x��Ľ�������Ϊ����1��0������3��0����
��ͼ��

��2�������ߵĶԳ���Ϊֱ��x=1��
��x1��x2��1����
��y1��y2��
�ʴ�Ϊy1��y2��
��3����ͼ��x1��x2Ϊ����x2��2x��1=0��������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������б���Ķ�Ӧֵ��
x | 3.23 | 3.24 | 3.25 | 3.26 |
| ��0.06 | ��0.02 | 0.03 | 0.09 |
д������![]() (a��0��a��b��cΪ����)һ����x�ķ�Χ��__��
(a��0��a��b��cΪ����)һ����x�ķ�Χ��__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������й���һ��![]() Ԫ/ǧ�˵���ɫʳƷ�������
Ԫ/ǧ�˵���ɫʳƷ�������![]() Ԫ/ǧ�����ۣ���ôÿ����۳�
Ԫ/ǧ�����ۣ���ôÿ����۳�![]() ǧ�ˣ������۾���֪��ÿ��������
ǧ�ˣ������۾���֪��ÿ��������![]() ��ǧ�ˣ������۵���
��ǧ�ˣ������۵���![]() ��Ԫ��
��Ԫ��![]() ��������ͼ��ʾ��һ�κ�����ϵ��
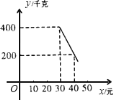
��������ͼ��ʾ��һ�κ�����ϵ��
![]() �����
�����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
![]() �����������������۸���ɫʳƷÿ��������Ϊ
�����������������۸���ɫʳƷÿ��������Ϊ![]() Ԫ�������۵���Ϊ��ֵʱ��ÿ��ɻ�����������������Ƕ��٣�
Ԫ�������۵���Ϊ��ֵʱ��ÿ��ɻ�����������������Ƕ��٣�
![]() �����г����飬����ɫʳƷÿ��ɻ�������
�����г����飬����ɫʳƷÿ��ɻ�������![]() Ԫ���ָó��о���Ҫ��ÿ�����õ���
Ԫ���ָó��о���Ҫ��ÿ�����õ���![]() Ԫ����������ó���ȷ����ɫʳƷ���۵���
Ԫ����������ó���ȷ����ɫʳƷ���۵���![]() �ķ�Χ��ֱ��д������
�ķ�Χ��ֱ��д������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��������������������y=ax2+bx+l��x����������ͬ�Ľ���A��B����A��B��ԭ��ľ��붼С��1����a+b����Сֵ���ڣ�������
A. 16 B. 10 C. 4 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OAB�Ķ���A��B������ֱ�Ϊ��4��0������4��n������������O��A��������y=��x2+bx+c�Ķ���C���ڱ�OB�ϣ���ͼ����Ӱ����ͼ�ε������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������Rt��ABC������Rt��ADE��AB��AC��AD��AE��AB��AC��AD��AE��CD��AE��BE�ֱ��ڵ�M��F��

��1����֤����DAC�ա�EAB.
��2����֤��CD��BE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
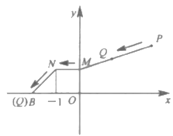
����Ŀ����ͼ����֪![]() ��
��![]() ����
����![]() ��
��![]() ����������ƶ���
����������ƶ���![]() ���ϵĵ�
���ϵĵ�![]() �������ش�ֱ��
�������ش�ֱ��![]() ��ķ��������ƶ�1����λ����
��ķ��������ƶ�1����λ����![]() ��������ƶ�����
��������ƶ�����![]() ��ֹͣ.����
��ֹͣ.����![]() �ƶ���·�����ʱ (�������߶�
�ƶ���·�����ʱ (�������߶�![]() ��
��![]() ��
��![]() ����֮����С)����
����֮����С)����![]() ������Ϊ�� ��
�������� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x�ύ��A��-3��0����B��1��0�����㣬��y���ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��
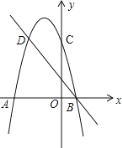
��1�����D���꼰���κ����Ľ���ʽ��
��2������ͼ��ֱ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��D��E�ֱ�����ABC�ı�BA��BC�ӳ����ϵĵ㣬����DAC��ƽ����AF����AF��BC��

��1����֤����ABC�ǵ��������Σ�
��2������ACE��ƽ���߽�AF�ڵ�G������B��40�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com