
【题目】如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
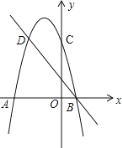
(1)求点D坐标及二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
【答案】(1)D(-2,3);y=![]() -2x+3;(2)x<-2或x>1.
-2x+3;(2)x<-2或x>1.
【解析】
(1)根据抛物线的对称性来求点D的坐标;设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),把点A、B、C的坐标分别代入函数解析式,列出关于系数a、b、c的方程组,通过解方程组求得它们的值即可;(2)根据图象直接写出答案.
(1)∵如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,
∴对称轴是x=![]() -3=-1.
-3=-1.
又点C(0,3),点C、D是二次函数图象上的一对对称点,
∴D(-2,3);
设二次函数的解析式为y=![]() +bx+c(a≠0,a、b、c常数),
+bx+c(a≠0,a、b、c常数),
根据题意得, ,
,
解得 a=-1,b=-2,c=3,
所以二次函数的解析式为y=![]() -2x+3;
-2x+3;
(2)如图,一次函数值大于二次函数值的x的取值范围是x<-2或x>1.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形.
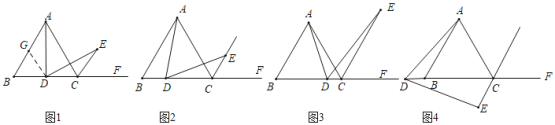
(1)如图1,点D是边BC的中点,∠ADE=60°,且DE交△ABC外角∠ACF的平分线CE于点E,求证:AD=DE;(提示:取AB的中点G,连接DG)
(2)小颖对(1)题进行了探索:如果将(1)题中的“点D是边BC的中点”改为“点D是直线BC上任意一点(B、C两点除外)”,其它条件不变,结论AD=DE是否仍然成立?小颖将点D的位置分为三种情形,画出了图2、图3、图4,现在请你在图2、图3、图4中选择一种情形,帮小颖验证:结论AD=DE是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3
(1)请你把已知的二次函数化成y=(x﹣h)2+k的形式,并在平面直角坐标系中画出它的图象;
(2)如果A(x1,y1)、B(x2,y2)是(1)中像上的两点,且x1<x2<1,请直接写出y1、y2的大小关系为 .
(3)利用(1)中的图象表示出方程x2﹣2x﹣1=0的根,画在(1)的图象上即可,要求保留画图痕迹.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 、
、![]() 两个圆柱形容器放置在同一水平桌面上,开始时容器
两个圆柱形容器放置在同一水平桌面上,开始时容器![]() 中盛满水,容器
中盛满水,容器![]() 中盛有高度为1 dm的水,容器
中盛有高度为1 dm的水,容器![]() 下方装有一只水龙头,容器
下方装有一只水龙头,容器![]() 向容器
向容器![]() 匀速注水.设时间为t (s),容器
匀速注水.设时间为t (s),容器![]() 、
、![]() 中的水位高度
中的水位高度![]() (dm)、
(dm)、![]() (dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
(dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
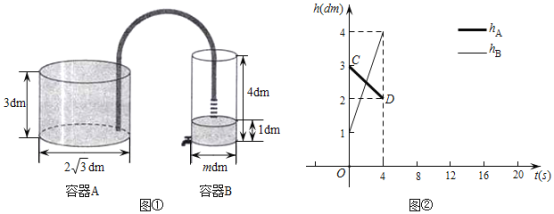
(1)容器![]() 向容器
向容器![]() 注水的速度为 dm3/s(结果保留
注水的速度为 dm3/s(结果保留![]() ),容器
),容器![]() 的底面直径
的底面直径![]() dm;
dm;
(2)当容器![]() 注满水后,容器
注满水后,容器![]() 停止向容器
停止向容器![]() 注水,同时开启容器
注水,同时开启容器![]() 的水龙头进行放水,放水速度为
的水龙头进行放水,放水速度为![]() dm3/s.请在图②中画出容器
dm3/s.请在图②中画出容器![]() 中水位高度
中水位高度![]() 与时间 (
与时间 (![]() )的函数图像,说明理由;
)的函数图像,说明理由;
(3)当容器B注满水后,容器A继向容器B注水,同时开启容器B的水龙头进行放水,放水速度为![]() dm3/s,直至容器
dm3/s,直至容器![]() 、
、![]() 水位高度相同时,立即停止放水和注水,求容器
水位高度相同时,立即停止放水和注水,求容器![]() 向容器
向容器![]() 全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量y与销售单价x之间的关系可以近似地看作一次函数:y=﹣5x+150,物价部门规定这种笔记本每本的销售单价不得高于18元.
(1)当每月销售量为70本时,获得的利润为多少元;
(2)该文具店这种笔记本每月获得利润为W元,求每月获得的利润W元与销售单价x之间的函数关系式,并写出自变量的取值范围;
(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.
,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 港口位于
港口位于![]() 观测点北偏东
观测点北偏东![]() 方向,且其到
方向,且其到![]() 观测点正北方向的距离
观测点正北方向的距离![]() 的长为
的长为![]() ,一艘货轮从
,一艘货轮从![]() 港口以
港口以![]() 的速度沿如图所示的
的速度沿如图所示的![]() 方向航行,
方向航行,![]() 后达到
后达到![]() 处,现测得
处,现测得![]() 处位于
处位于![]() 观测点北偏东
观测点北偏东![]() 方向,求此时货轮与
方向,求此时货轮与![]() 观测点之间的距离
观测点之间的距离![]() 的长(精确到
的长(精确到![]() ).(参考数据:
).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
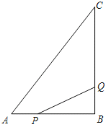
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
![]() 点
点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() ,
,![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
![]() 若
若![]() 点沿射线
点沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,点
的速度移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动,![]() 、
、![]() 同时出发,问几秒后,
同时出发,问几秒后,![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com