
【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
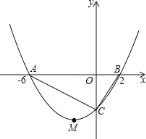
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() .
.
【解析】
(1)根据顶点坐标公式即可求得a、b、c的值,即可解题;
(2)易求得点B、C的坐标,即可求得OC的长,即可求得![]() 的面积,即可解题;
的面积,即可解题;
(3)作PE⊥x轴于点E,交AC于点F,可将![]() 的面积转化为
的面积转化为![]() 和
和![]() 的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示
的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示![]() 的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
![]() 设此函数的解析式为
设此函数的解析式为![]() ,
,
∵函数图象顶点为![]() ,
,
∴![]() ,
,
又∵函数图象经过点![]() ,
,
∴![]()
解得![]() ,
,
∴此函数的解析式为![]() ,即
,即![]() ;
;
![]() ∵点
∵点![]() 是函数
是函数![]() 的图象与
的图象与![]() 轴的交点,
轴的交点,
∴点![]() 的坐标是
的坐标是![]() ,
,
又当![]() 时,有
时,有![]() ,
,
解得![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
则![]() ;
;
![]() 假设存在这样的点,过点
假设存在这样的点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .
.
设![]() ,则
,则![]() ,
,

设直线![]() 的解析式为
的解析式为![]() ,
,
∵直线![]() 过点
过点![]() ,
,![]() ,
,
∴![]() ,
,
解得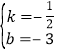 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
∴![]()
![]()
![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
此时点![]() 的坐标是
的坐标是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,![]() 、
、![]() 两个圆柱形容器放置在同一水平桌面上,开始时容器
两个圆柱形容器放置在同一水平桌面上,开始时容器![]() 中盛满水,容器
中盛满水,容器![]() 中盛有高度为1 dm的水,容器
中盛有高度为1 dm的水,容器![]() 下方装有一只水龙头,容器
下方装有一只水龙头,容器![]() 向容器
向容器![]() 匀速注水.设时间为t (s),容器
匀速注水.设时间为t (s),容器![]() 、
、![]() 中的水位高度
中的水位高度![]() (dm)、
(dm)、![]() (dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
(dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
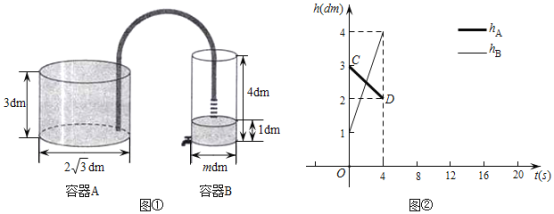
(1)容器![]() 向容器
向容器![]() 注水的速度为 dm3/s(结果保留
注水的速度为 dm3/s(结果保留![]() ),容器
),容器![]() 的底面直径
的底面直径![]() dm;
dm;
(2)当容器![]() 注满水后,容器
注满水后,容器![]() 停止向容器
停止向容器![]() 注水,同时开启容器
注水,同时开启容器![]() 的水龙头进行放水,放水速度为
的水龙头进行放水,放水速度为![]() dm3/s.请在图②中画出容器
dm3/s.请在图②中画出容器![]() 中水位高度
中水位高度![]() 与时间 (
与时间 (![]() )的函数图像,说明理由;
)的函数图像,说明理由;
(3)当容器B注满水后,容器A继向容器B注水,同时开启容器B的水龙头进行放水,放水速度为![]() dm3/s,直至容器
dm3/s,直至容器![]() 、
、![]() 水位高度相同时,立即停止放水和注水,求容器
水位高度相同时,立即停止放水和注水,求容器![]() 向容器
向容器![]() 全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 港口位于
港口位于![]() 观测点北偏东
观测点北偏东![]() 方向,且其到
方向,且其到![]() 观测点正北方向的距离
观测点正北方向的距离![]() 的长为
的长为![]() ,一艘货轮从
,一艘货轮从![]() 港口以
港口以![]() 的速度沿如图所示的
的速度沿如图所示的![]() 方向航行,
方向航行,![]() 后达到
后达到![]() 处,现测得
处,现测得![]() 处位于
处位于![]() 观测点北偏东
观测点北偏东![]() 方向,求此时货轮与
方向,求此时货轮与![]() 观测点之间的距离
观测点之间的距离![]() 的长(精确到
的长(精确到![]() ).(参考数据:
).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC的平分线与∠ACD的平分线交于点A![]() ,∠A
,∠A![]() BC的平分线与∠A
BC的平分线与∠A![]() CD的平分线交于点A
CD的平分线交于点A![]() ,以此类推,∠A
,以此类推,∠A![]() BC的平分线与∠A
BC的平分线与∠A![]() CD的平分线交于点A
CD的平分线交于点A![]() ,则∠A
,则∠A![]() 的大小是___
的大小是___

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿
沿![]() 折叠压平,使点
折叠压平,使点![]() 落在坐标平面内,设点
落在坐标平面内,设点![]() 的对应点为点
的对应点为点![]() .若抛物线
.若抛物线![]() (
(![]() 且
且![]() 为常数)的顶点落在
为常数)的顶点落在![]() 的内部,则
的内部,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为![]() 元的苹果,物价部门规定每箱售价不得高于
元的苹果,物价部门规定每箱售价不得高于![]() 元,市场调查发现,若每箱以
元,市场调查发现,若每箱以![]() 元的价格销售,平均每天销售
元的价格销售,平均每天销售![]() 箱,价格每提高
箱,价格每提高![]() 元,平均每天少销售
元,平均每天少销售![]() 箱.
箱.
求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
(元/箱)之间的函数关系式.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
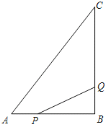
![]() 点
点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() ,
,![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
![]() 若
若![]() 点沿射线
点沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,点
的速度移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动,![]() 、
、![]() 同时出发,问几秒后,
同时出发,问几秒后,![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
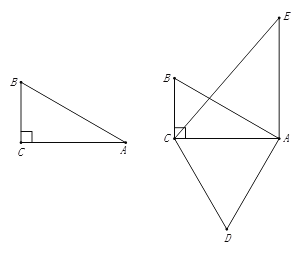
【题目】如图1,直角三角形ABC中,∠C=90°,CB=1,∠BAC=30°.
(1)求AB、AC的长;
(2)如图2,将AB绕点A顺时针旋转60°得到线段AE,将AC绕点A逆时针旋转60°得到线段AD.
①连接CE,BD.求证:BD=EC;
②连接DE交AB于F,请你作出符合题意的图形并求出DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一透明的口袋中装有![]() 个球,这
个球,这![]() 个球分别标有
个球分别标有![]() ,
,![]() ,
,![]() ,这些球除了数字外都相同.
,这些球除了数字外都相同.
![]() 如果从袋子中任意摸出一个球,那么摸到标有数字是
如果从袋子中任意摸出一个球,那么摸到标有数字是![]() 的球的概率是多少?
的球的概率是多少?
![]() 如果一次摸两个球,用树状图或列表法求出摸到的两个球标有的数字的积为奇数的概率;
如果一次摸两个球,用树状图或列表法求出摸到的两个球标有的数字的积为奇数的概率;
![]() 小明和小亮玩摸球游戏,游戏的规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小亮随机摸出一个球,记下数字.谁摸出的球的数字大,谁获胜.请你用树状图或列表法分析游戏规则对双方是否公平?并说明理由.
小明和小亮玩摸球游戏,游戏的规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小亮随机摸出一个球,记下数字.谁摸出的球的数字大,谁获胜.请你用树状图或列表法分析游戏规则对双方是否公平?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com