
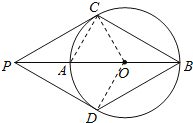
【题目】如图,![]() 为
为![]() 的直径
的直径![]() 延长线上的一点,
延长线上的一点,![]() 与
与![]() 相切,切点为
相切,切点为![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() .已知
.已知![]() .下列结论:
.下列结论:
![]() 与
与![]() 相切;
相切;![]() 四边形
四边形![]() 是菱形;
是菱形;![]() ;
;![]() .
.
其中正确的个数为( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
【答案】A
【解析】
(1)利用切线的性质得出∠PCO=90°,进而得出△PCO≌△PDO(SSS),即可得出∠PCO=∠PDO=90°,得出答案即可;(2)利用(1)所求得出:∠CPB=∠BPD,进而求出△CPB≌△DPB(SAS),即可得出答案;(3)利用全等三角形的判定得出△PCO≌△BCA(ASA),进而得出CO=12PO=12AB;(4)利用四边形PCBD是菱形,∠CPO=30°,则DP=DB,则∠DPB=∠DBP=30°,求出即可.
(1)连接CO,DO,
∵PC与⊙O相切,切点为C,
∴![]()
在△PCO和△PDO中,
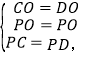
∴△PCO≌△PDO(SSS),
∴![]() ∴PD与⊙O相切,
∴PD与⊙O相切,
故(1)正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,
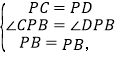
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故(2)正确;
(3)连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴![]()
在△PCO和△BCA中,
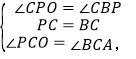
∴△PCO≌△BCA(ASA),
∴AC=CO,
∴AC=CO=AO,
∴![]()
∴![]()
∴![]()
∴PO=AB,
故(3)正确;
(4)∵四边形PCBD是菱形,![]()
∴DP=DB,则![]()
∴![]() 故(4)正确;
故(4)正确;
正确个数有4个,
故选:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=﹣x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
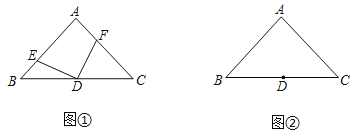
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF.
①求证:BE=AF;
②若S△BDE=![]() S△ABC=2,求S△CDF;
S△ABC=2,求S△CDF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF.
①BE=AF还成立吗?请利用图②说明理由;
②若S△BDE=![]() S△ABC=8,直接写出DF的长.
S△ABC=8,直接写出DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…分别在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B1B2A2,△B2A2A3,△B2B3A3…,都是等腰直角三角形,如果OA1=1,则点A2019的坐标为_____.
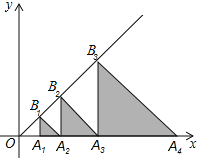
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.

(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图1所示,直线y=x+c与x轴交于点A(﹣4,0),与y轴交于点C,抛物线y=﹣x2+bx+c经过点A,C.
(1)求抛物线的解析式
(2)点E在抛物线的对称轴上,求CE+OE的最小值;
(3)如图2所示,M是线段OA的上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N
①若以C,P,N为顶点的三角形与△APM相似,则△CPN的面积为 ;
②若点P恰好是线段MN的中点,点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC'、△BCA'、△CAB'都是△ABC形外的等边三角形,而点D在AC上,且BC=DC
(1)证明:△C'BD≌△B'DC
(2)证明:△AC'D≌△DB'A
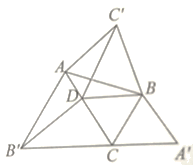
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com