
(2014•白银)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
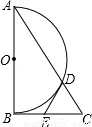
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:2016届河北省保定市竞秀区九年级上学期期末数学试卷(解析版) 题型:选择题
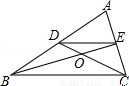
(2015秋•保定期末)如图,D,E分别是△ABC的边AB,AC上的中点,CD与BE交于点O,则S△DOE:S△BOC的值为( )
A.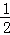 B.
B. C.
C.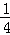 D.
D.
查看答案和解析>>
科目:初中数学 来源:2016届北京市顺义区九年级上学期期末数学试卷(解析版) 题型:解答题
(2012•大连)如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
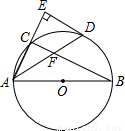
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源:2016届北京市顺义区九年级上学期期末数学试卷(解析版) 题型:选择题
(2012•黄石)如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( )
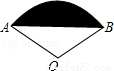
A.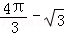 B.
B.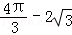 C.
C.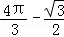 D.
D.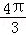
查看答案和解析>>
科目:初中数学 来源:2016届北京市顺义区九年级上学期期末数学试卷(解析版) 题型:选择题
(2014•绍兴)不等式3x+2>﹣1的解集是( )
A.x>﹣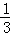 B.x<﹣
B.x<﹣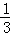 C.x>﹣1 D.x<﹣1
C.x>﹣1 D.x<﹣1
查看答案和解析>>
科目:初中数学 来源:2016届安徽省黄山市九年级上学期期末数学试卷(解析版) 题型:解答题
(2015秋•黄山期末)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
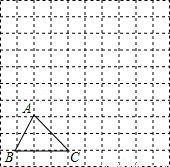
(1)先将△ABC竖直向上平移6个单位,再水平向右平移1个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求(2)中点A1旋转到点A2所经过的弧长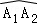 (结果保留π).
(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2016届安徽省黄山市九年级上学期期末数学试卷(解析版) 题型:选择题
(2015秋•黄山期末)将抛物线y=(x﹣1)2+3向右平移1个单位,再向上平移3个单位后所得抛物线的表达式为( )
A.y=(x﹣2)2 B.y=x2 C.y=x2+6 D.y=(x﹣2)2+6
查看答案和解析>>
科目:初中数学 来源:2015-2016学年山东省烟台市龙口市八年级上学期期末数学试卷(解析版) 题型:解答题
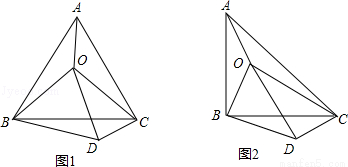
(2015秋•龙口市期末)(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=3,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:
①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com