
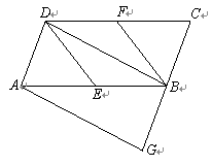
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ8ЕФе§ЗНаЮOABCЕФСНБпдкзјБъжсЩЯЃЌвдЕуCЮЊЖЅЕуЕФХзЮяЯпОЙ§ЕуAЃЌЕуPЪЧХзЮяЯпЩЯЕуAЁЂCМфЕФвЛИіЖЏЕуЃЈКЌЖЫЕуЃЉЃЌЙ§ЕуPзїPFЁЭBCгкЕуFЃЌЕуDЁЂEЕФзјБъЗжБ№ЮЊЃЈ0ЃЌ6ЃЉЃЌЃЈЉ4ЃЌ0ЃЉЃЌСЌНгPDЃЌPEЃЌDEЃЎ
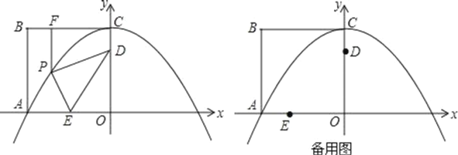
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉаЁУїЬНОПЕуPЕФЮЛжУЪЧЗЂЯжЃКЕБЕуPгыЕуAЛђЕуCжиКЯЪБЃЌPDгыPFЕФВюЮЊЖЈжЕЃЌНјЖјВТЯыЃКЖдгкШЮвтвЛЕуPЃЌPDгыPFЕФВюЮЊЖЈжЕЃЌЧыФуХаЖЈИУВТЯыЪЧЗёе§ШЗЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЧыжБНгаДГіЁїPDEжмГЄЕФзюДѓжЕКЭзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2+8ЃЛЃЈ2ЃЉе§ШЗЃЌdЃН|PDЉPF|ЮЊЖЈжЕ2ЃЛРэгЩМћНтЮіЃЛЃЈ3ЃЉЁїPDEжмГЄЕФзюДѓжЕЪЧ2
x2+8ЃЛЃЈ2ЃЉе§ШЗЃЌdЃН|PDЉPF|ЮЊЖЈжЕ2ЃЛРэгЩМћНтЮіЃЛЃЈ3ЃЉЁїPDEжмГЄЕФзюДѓжЕЪЧ2![]() +14ЃЌзюаЁжЕЪЧ2
+14ЃЌзюаЁжЕЪЧ2![]() +10ЃЎ
+10ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпНтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉЪзЯШБэЪОГіPЃЌFЕузјБъЃЌдйРћгУСНЕужЎМфОрРыЙЋЪНЕУГіPDЃЌPFЕФГЄЃЌНјЖјЧѓГіМДПЩЃЛ
ЃЈ3ЃЉЙ§EзїEFЁЭxжсЃЌНЛХзЮяЯпгкЕуPЃЌЧѓЕУCЁїPDEЃНEDЃЋPEЃЋPDЃНEDЃЋPEЃЋPFЃЋ2ЃНEDЃЋ2ЃЋЃЈPEЃЋPFЃЉЃЌЕБPЁЂEЁЂFШ§ЕуЙВЯпЪБЃЌPEЃЋPFзюаЁЃЛЕБPгыAжиКЯЪБЃЌPEЃЋPFзюДѓЃЛМДПЩНтД№ЃЎ
ЃЈ1ЃЉЁпБпГЄЮЊ8ЕФе§ЗНаЮOABCЕФСНБпдкзјБъжсЩЯЃЌвдЕуCЮЊЖЅЕуЕФХзЮяЯпОЙ§ЕуAЃЌ
ЁрCЃЈ0ЃЌ8ЃЉЃЌAЃЈЉ8ЃЌ0ЃЉЃЌ
ЩшХзЮяЯпНтЮіЪНЮЊЃКyЃНax2+cЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУЃК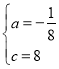 ЃЎ
ЃЎ
ЁрХзЮяЯпНтЮіЪНЮЊyЃНЉ![]() x2+8ЃЎ
x2+8ЃЎ
ЃЈ2ЃЉЩшPЃЈxЃЌЉ![]() x2+8ЃЉЃЌдђFЃЈxЃЌ8ЃЉЃЌ
x2+8ЃЉЃЌдђFЃЈxЃЌ8ЃЉЃЌ
дђPFЃН8ЉЃЈЉ![]() x2+8ЃЉЃН
x2+8ЃЉЃН![]() x2ЃЎ
x2ЃЎ
PD2ЃНx2+[6ЉЃЈЉ![]() x2+8ЃЉ]2ЃН
x2+8ЃЉ]2ЃН![]() x4+
x4+![]() x2+4ЃНЃЈ
x2+4ЃНЃЈ![]() x2+2ЃЉ2
x2+2ЃЉ2
ЁрPDЃН![]() x2+2ЃЌ
x2+2ЃЌ
ЁрdЃН|PDЉPF|ЃН|![]() x2+2Љ
x2+2Љ![]() x2|ЃН2
x2|ЃН2
ЁрdЃН|PDЉPF|ЮЊЖЈжЕ2ЃЛ
ЃЈ3ЃЉШчЭМЃЌЙ§ЕуEзїEFЁЭxжсЃЌНЛХзЮяЯпгкЕуPЃЌ
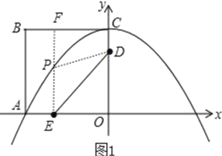
гЩdЃН|PDЉPF|ЮЊЖЈжЕ2ЃЌ
ЕУCЁїPDEЃНED+PE+PDЃНED+PE+PF+2ЃНED+2+ЃЈPE+PFЃЉЃЌ
гжЁпDЃЈ0ЃЌ6ЃЉЃЌEЃЈЉ4ЃЌ0ЃЉ
ЁрDEЃН![]() ЃЎ
ЃЎ
ЁрCЁїPDEЃН2![]() +2+ЃЈPE+PFЃЉЃЌ
+2+ЃЈPE+PFЃЉЃЌ
ЕБPEКЭPFдкЭЌвЛжБЯпЪБPE+PFзюаЁЃЌ
ЕУCЁїPDEзюаЁжЕЃН2![]() +2+8ЃН2
+2+8ЃН2 ![]() +10ЃЎ
+10ЃЎ
ЩшPЮЊХзЮяЯпACЩЯвьгкЕуAЕФШЮвтвЛЕуЃЌЙ§PзїPMЁЮxжсЃЌНЛABгкЕуMЃЌСЌНгMEЃЌШчЭМ2ЃЎ
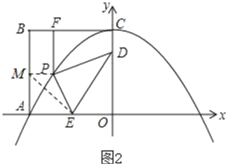
гЩгкEЪЧAOЕФжаЕуЃЌвзжЄЕУMEЁнPEЃЈЕБЕуPНгНќЕуAЪБЃЌдкЁїPMEжаЃЌЯдШЛЁЯMPEЪЧЖлНЧЃЌЙЪMEЁнPEЃЌгыAжиКЯЪБЃЌЕШКХГЩСЂЃЉЃЌЖјMEЁмAE+AMЃЌ
ЫљвдPEЁмAE+AMЃЎ
ЫљвдЕБPгыAжиКЯЪБЃЌPE+PFзюДѓЃЌ
AEЃН8Љ4ЃН4ЃЌPDЃН![]() ЃН10ЃЎ
ЃН10ЃЎ
ЕУCЁїPDEзюДѓжЕЃН2![]() +4+10ЃН2
+4+10ЃН2![]() +14ЃЎ
+14ЃЎ
злЩЯЫљЪіЃЌЁїPDEжмГЄЕФзюДѓжЕЪЧ2![]() +14ЃЌзюаЁжЕЪЧ2
+14ЃЌзюаЁжЕЪЧ2![]() +10ЃЎ
+10ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬmx2Љ2xЉ1ЃН0гаСНИіЪЕЪ§Иљx1ЃЌx2ЃЎ
ЃЈ1ЃЉЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБx12+x22ЃНЉ6x1x2ЪБЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁѕABCDжаЃЌEЁЂFЗжБ№ЮЊБпABЁЂCDЕФжаЕуЃЌBDЪЧЖдНЧЯпЃЌAGЁЮDBНЛCBЕФбгГЄЯпгкGЃЎШєЫФБпаЮBEDFЪЧСтаЮЃЌдђЫФБпаЮAGBDЪЧЪВУДЬиЪтЫФБпаЮЃПВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкВтСПЁАКгСїПэЖШЁБЕФзлКЯгыЪЕМљЛюЖЏжаЃЌаЁРюЭЌбЇЩшМЦЕФЗНАИМАВтСПЪ§ОнШчЯТЃКдкКгЖдАЖБпбЁЖЈвЛИіФПБъЕуAЃЌдкНќАЖШЁЕуBЃЌCЃЌD (ЕуBЃЌCЃЌDдкЭЌвЛЬѕжБЯпЩЯ)ЃЌABЁЭBDЃЌЁЯACBЃН45ЁуЃЌCDЃН20УзЃЌЧвЃЎШєВтЕУЁЯADBЃН25ЁуЃЌЧыФуАяжњаЁРюЧѓКгЕФПэЖШAB.ЃЈsin25ЁуЁж0.42ЃЌcos25ЁуЁж0.91ЃЌtan25ЁуЁж0.47ЃЌНсЙћОЋШЗЕН0.1УзЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
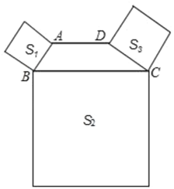
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯABC+ЁЯDCBЃН90ЁуЃЌЧвBCЃН2ADЃЌвдABЁЂBCЁЂDCЮЊБпЯђЭтзїе§ЗНаЮЃЌЦфУцЛ§ЗжБ№ЮЊS1ЁЂS2ЁЂS3ЃЌШєS1ЃН2ЃЌS3ЃН4ЃЌдђS2ЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЕЭЬМЩњЛюЃЌТЬЩЋГіааЁБЪЧЮвУЧГЋЕМЕФвЛжжЩњЛюЗНЪНЃЌФГаЃЮЊСЫНтбЇЩњЖдЙВЯэЕЅГЕЕФЪЙгУЧщПіЃЌЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌВЂНЋетДЮЕїВщЕФНсЙћЛцжЦСЫвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
ИљОнЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉmЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉетДЮЕїВщНсЙћЕФжкЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ4ЃЉвбжЊШЋаЃЙВ3000УћбЇЩњЃЌЧыЙРМЦЁАОГЃЪЙгУЁБЙВЯэЕЅГЕЕФбЇЩњДѓдМгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁбOжа,ЕуCЪЧгХЛЁACBЕФжаЕу,DЁЂEЗжБ№ЪЧOAЁЂOBЩЯЕФЕу,ЧвAD=BE,ЯвCMЁЂCNЗжБ№Й§ЕуDЁЂE.
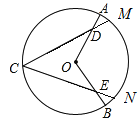
(1)ЧѓжЄЃКCD=CEЃЎ
(2)ЧѓжЄЃК![]() =
=![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌгУРщАЪППЧНЮЇГЩОиаЮЛЈЮЇABCDЃЌЧНПЩРћгУЕФзюДѓГЄЖШЮЊ15УзЃЌвЛУцРћгУОЩЧНЃЌЦфгрШ§УцгУРщАЪЮЇГЩЃЌРщАЪзмГЄЮЊ24УзЃЎ
(1)ШєЮЇГЩЕФЛЈЦдУцЛ§ЮЊ40Уз2ЪБЃЌЧѓBCЕФГЄЃЛ
(2)ШчЭМ2ШєМЦЛЎдкЛЈЦджаМфгУвЛЕРИєГЩСНИіаЁОиаЮЃЌЧвЮЇГЩЕФЛЈЦдУцЛ§ЮЊ50Уз2ЃЌЧыФуХаЖЯФмЗёГЩЙІЮЇГЩЛЈЦдЃЌШчЙћФмЃЌЧѓBCЕФГЄЃПШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїВЮМгФГИіжЧСІОКД№НкФПЃЌД№ЖдзюКѓСНЕРЕЅбЁЬтОЭЫГРћЭЈЙиЃЎЕквЛЕРЕЅбЁЬтга3ИібЁЯюЃЌЕкЖўЕРЕЅбЁЬтга4ИібЁЯюЃЌетСНЕРЬтаЁУїЖМВЛЛсЃЌВЛЙ§аЁУїЛЙгавЛИіЁАЧѓжњЁБУЛгагУЃЈЪЙгУЁАЧѓжњЁБПЩвдШУжїГжШЫШЅЕєЦфжавЛЬтЕФвЛИіДэЮѓбЁЯюЃЉЃЎ
ЃЈ1ЃЉШчЙћаЁУїЕквЛЬтВЛЪЙгУЁАЧѓжњЁБЃЌФЧУДаЁУїД№ЖдЕквЛЕРЬтЕФИХТЪЪЧЁЁЁЁЃЎ
ЃЈ2ЃЉШчЙћаЁУїНЋЁАЧѓжњЁБСєдкЕкЖўЬтЪЙгУЃЌЧыгУЪїзДЭМЛђепСаБэРДЗжЮіаЁУїЫГРћЭЈЙиЕФИХТЪЃЎ
ЃЈ3ЃЉДгИХТЪЕФНЧЖШЗжЮіЃЌФуНЈвщаЁУїдкЕкМИЬтЪЙгУЁАЧѓжњЁБЃЎЃЈжБНгаДГіД№АИЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com