练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．早晨8：45时，时钟的分针与时针的夹角是多少度？

    分析 因为钟表上的刻度是把一个圆平均分成了12等份，每一份是30°，借助图形，找出时针和分针之间相差的大格数，用大格数乘30°即可．

    解答 解：∵时针在钟面上每分钟转0.5°，分针每分钟转6°，
    ∴钟表上8：45时，时针与分针的夹角可以看成时针转过8时0.5°×45=22.5°，分针在数字9上．
    ∵钟表12个数字，每相邻两个数字之间的夹角为30°，
    ∴8：45时分针与时针的夹角30°-12.5°=7.5°．

    点评 本题考查钟表分针所转过的角度计算．在钟表问题中，常利用时针与分针转动的度数关系：分针每转动1°时针转动（$\frac{1}{12}$）°，并且利用起点时间时针和分针的位置关系建立角的图形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．解方程：$\frac{1+x}{2-x}-1=\frac{1}{x-2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

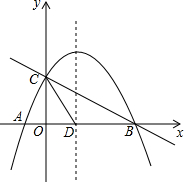    12．如图，直线y1=-$\frac{1}{2}$x+2与x轴，y轴分别交于B，C，抛物线y=ax2+bx+c（a≠0）经过点A，B，C，点A坐标为（-1，0）．
    （1）求抛物线的解析式；
    （2）抛物线的对称轴与x轴交于点D，连接CD，点P是直线BC上方抛物线上的一动点（不与B，C重合），当点P运动到何处时，四边形PCDB的面积最大？求出此时四边形PCDB面积的最大值和点P坐标；
    （3）在抛物线上的对称轴上是否存在一点Q，使△QCD是以CD为腰的等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知二次函数y=x2-2x+1的图象顶点为A，二次函数y=a（x-m-1）2+m2的图象经过点A，m≠0．
    （1）求a的值；
    （2）二次函数y=a（x-m-1）2+m2与x轴的两个交点和这个函数的顶点能否构成直角三角形？若能，请求出m的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知二次函数y=x2+（2a+1）x+（a-2）2，a取何值时：
    （1）抛物线与x轴有两个交点？
    （2）抛物线与x轴只有一个交点？
    （3）抛物线与x轴无交点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先化简，再求值：已知（a+b）2+（a-b）（2a+b）-3a2，其中a=-2，b=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．用配方法求当x为何值时，代数式x2-7x+2有最小值，并求出这个最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．“十•一”黄金周期间，九寨沟风景区在7天假期中每天旅游的人数变化如表：（正数表示比9月30日多的人数，负数表示比9月30日少的人数）：
    日期10月1日10月2日10月3日10月4日10月5日10月6日10月7日
    人数变化
    （万人）    		+1.7+0.9+0.4-0.4-0.8+0.2-1.2
    （1）若9月30日的游客人数记为a万人，请用含a的代数式表示10月2日的游客人数；
    （2）请判断7天内游客人数最多和最少的各是哪一天，它们相差多少万人？
    （2）若a=2，平均每人消费300元，请问风景区在这7天内总收入多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（　　）
    A．$y=\frac{9}{2x}$B．$y=\frac{2}{9x}$C．$y=\frac{{\sqrt{13}}}{x}$D．$y=\frac{{\sqrt{13}}}{2x}$

    查看答案和解析>>

    同步练习册答案