Question

10．如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上的一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴．直线OB于点E、F，点E为垂足，连结CF．
（1）当∠AOB=30°时，求弧AB的长；
（2）当DE=8时，求过点O、A、F的抛物线的解析式；
（3）在点B运动过程中，点E在线段OA上时，是否存在以点E、C、F为顶点的三角形与△AOB相似？若存在，请求出此时点E的坐标；若不存在，请说明理由．

Answer 1

分析 （1）连接BC，由已知得∠ACB=2∠AOB=60°，AC=$\frac{1}{2}$AO=5，根据弧长公式求解；
（2）连接OD，由垂直平分线的性质得OD=OA=10，又DE=8，在Rt△ODE中，由勾股定理求OE，依题意证明△OEF∽△DEA，利用相似比求EF，从而求出点F的坐标，利用待定系数法求出二次函数的解析式，即可解答；
（3）存在．当以点E、C、F为顶点的三角形与△AOB相似时，分为①当交点E在O，C之间时，由以点E、C、F为顶点的三角形与△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB，②当交点E在点C的右侧时，要使△ECF与△BAO相似，只能使∠ECF=∠BAO．

解答 解：（1）如图1，连接BC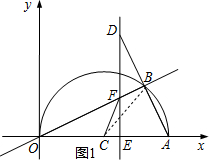

∵A（10，0），
∴OA=10，CA=5，
∵∠AOB=30°，
∴∠ACB=2∠AOB=60°，
∴弧AB的长=$\frac{60×π×5}{180}$=$\frac{5π}{3}$；
（2）①若D在第一象限，
如图2，连接OD，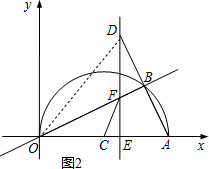

∵OA是⊙C直径
∴∠OBA=90°，
又∵AB=BD，
∴OB是AD的垂直平分线，
∴OD=OA=10，
在Rt△ODE中，
OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∴AE=AO-OE=10-6=4，
由∠AOB=∠ADE=90°-∠OAB，∠OEF=∠DEA，
得△OEF∽△DEA，
∴$\frac{AE}{DE}=\frac{EF}{OE}$，即$\frac{4}{8}=\frac{EF}{6}$，
∴EF=3；
∴点F的坐标为（6，4），
设过点O、A、F的抛物线的解析式为y=ax²+bx+c，
把点O（0，0），A（10，0），F（6，4）代入y=ax²+bx+c，
得：
$\left\{\begin{array}{l}{c=0}\\{100a+10b+c=0}\\{36a+6b+c=4}\end{array}\right.$
解得：$\left\{\begin{array}{l}{a=-\frac{1}{6}}\\{b=\frac{5}{3}}\\{c=0}\end{array}\right.$
∴y=-$\frac{1}{6}{x}^{2}+\frac{5}{3}x$
②若D在第二象限，
如图3，连接OD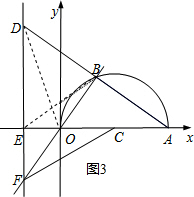

∵OA是⊙C直径，
∴∠OBA=90°，
又∵AB=BD，
∴OB是AD的垂直平分线，
∴OD=OA=10，
在Rt△ODE中，
OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∴AE=AO+OE=10+6=16，
由∠AOB=∠ADE=90°-∠OAB，∠OEF=∠DEA，
得△OEF∽△DEA，
∴$\frac{AE}{DE}=\frac{EF}{OE}$，即=$\frac{16}{8}=\frac{EF}{6}$，
∴EF=12；
∴点F的坐标为（-6，-12），
设过点O、A、F的抛物线的解析式为y=ax²+bx+c，
把点O（0，0），A（10，0），F（-6，-12）代入的：
$\left\{\begin{array}{l}{c=0}\\{100a+10b+c=0}\\{36a-6b+c=-12}\end{array}\right.$
解得：$\left\{\begin{array}{l}{a=-\frac{1}{8}}\\{b=\frac{5}{4}}\\{c=0}\end{array}\right.$
∴y=-$\frac{1}{8}{x}^{2}+\frac{5}{4}x$．
（3）设OE=x，
①如图4，当交点E在O，C之间时，由以点E、C、F为顶点的三角形与△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB，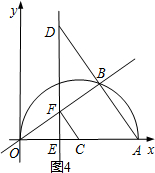

当∠ECF=∠BOA时，此时△OCF为等腰三角形，点E为OC
中点，即OE=$\frac{5}{2}$，
∴E₁（$\frac{5}{2}$，0）；
当∠ECF=∠OAB时，有CE=5-x，AE=10-x，
∴CF∥AB，有CF=$\frac{1}{2}$AB，
∵△ECF∽△EAD，
∴$\frac{CE}{AE}=\frac{CF}{AD}$，即$\frac{5-x}{10-x}=\frac{1}{4}$，解得：x=$\frac{10}{3}$，
∴E₂（$\frac{10}{3}$，0）；
②当交点E在点C的右侧时，
∵∠ECF＞∠BOA，
∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO
如图5，连接BE，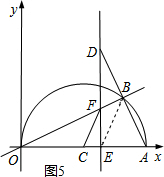

∵BE为Rt△ADE斜边上的中线，
∴BE=AB=BD，
∴∠BEA=∠BAO，
∴∠BEA=∠ECF，
∴CF∥BE，
∴$\frac{CF}{BE}=\frac{OC}{OE}$，
∵∠ECF=∠BAO，∠FEC=∠DEA=90°，
∴△CEF∽△AED，
∴$\frac{CF}{AD}=\frac{CE}{AE}$，
而AD=2BE，
∴$\frac{OC}{2OE}=\frac{CE}{AE}$，
即$\frac{5}{2x}=\frac{x-5}{10-x}$，
解得：${x}_{1}=\frac{5+5\sqrt{17}}{4}，{x}_{2}=\frac{5-5\sqrt{17}}{4}$＜0（舍去），
∴E₃（$\frac{5+5\sqrt{17}}{4}$，0）；
此时点E坐标为：E₁（$\frac{5}{2}$，0）、E₂（$\frac{10}{3}$，0）、E₃（$\frac{5+5\sqrt{17}}{4}$，0）．

点评 本题考查了相似三角形的判定与性质，勾股定理的运用，圆周角定理，弧长公式的运用．关键是理解题意，根据基本条件，图形的性质，分类求解．