Question

5．如图1，△ABC的两条中线AD、BE相交于点O
（1）求证：DO：AO=1：2；
（2）连接CO并延长交AB于F，求证：CF也是△ABC的中线；
（3）在（2）中，若∠A=90°，其它条件不变，连接DF交BE于K（如图2），连接ED，且△EDK∽△CAB，求AC：AB的值．

Answer 1

分析 （1）连接ED，可得ED为三角形ABC的中位线，利用中位线定理得到ED与AB平行，且等于AB的一半，进而得到三角形EOD与三角形AOB相似，且相似比为1：2，即可得证；
（2）设ED与CF交于点G，由三角形GOD与三角形AFO相似，由相似得比例，再由DG与AB平行，得比例，确定出AF=BF，即可得证；
（3）由∠A为直角，得到四边形AFDE为矩形，可得出三角形EDK与三角形BAE相似，再由三角形EDK与三角形CAB相似，得到三角形BAE与三角形CAB相似，由相似得比例，求出所求之比即可．

解答 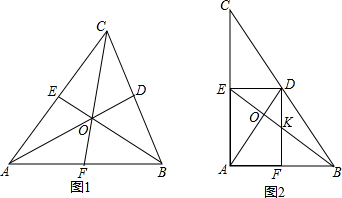（1）证明：连接ED，
∵E、D分别为AC、BC的中点，
∴ED∥AB，且ED=$\frac{1}{2}$AB，
∴△EDO∽△BAO，
∴DO：AO=ED：AB=1：2；
（2）证明：设CF交ED于点G，
由△DGO∽△AFO，得到DG：AF=DO：AO=1：2，
由DG∥AB得DG：BF=CD：CB=1：2，
∴DG：AF=DG：BF，
∴AF=BF，
∴AF也是△ABC的中线；
（3）解：由∠A=90°，得到四边形AFDE是矩形，
∴△EDK∽△BAE，
∵△EDK∽△CAB，
∴△BAE∽△CAB，
∴AE：AB=AB：AC，
∵AE=$\frac{1}{2}$AC，
∴AC：AB=$\sqrt{2}$．

点评 此题属于相似形综合题，涉及的知识有：相似三角形的判定与性质，三角形中位线定理，矩形的判定与性质，熟练掌握相似三角形的判定与性质是解本题的关键．