
【题目】如图在以点O为原点的数轴上,点A表示的数是3,点B在原点的左侧,且AB=6AO(我们把数轴上两点之间的距离用表示两点的大写字母一起标记,比如,点A与点B之间的距离记作AB).
(1)B点表示的数是_______.
(2)若动点P从O点出发,以每秒2个单位长度的速度匀速向左运动,问经过几秒钟后PA=3PB?并求出此时P点在数轴上对应的数.
(3)若动点M.P.N分别同时从A、O、B出发,匀速向右运动,其速度分别为1个单位长度/秒.2个单位长度/秒.4个单位长度/秒,设运动时间为t秒,请直接写出PM.PN.MN中任意两个相等时的时间.
![]()
【答案】(1)-15;(2)点P运动5.25秒,此时点P表示的数是-10.5或点P运动12秒,此时点P表示的数是-24;(3)当PM=PN时,t=12;当PM=MN时,t=7.5;当PN=MN时,t=3
【解析】
(1)A、B两点在原点两侧,则AB=OA+OB,知点A表示的数即OA 的长度,利用AB=6OA求出AB, 再用AB-OA即可求得OB的长,得到点B所表示的数
(2)点P由点O向左运动,可以在OB之间,也可以在点B左侧,所以应分两种情况;
(3)此问可理解为行程问题中的追及问题,两个点在运动t秒后的路程差为开始时的距离,依次即可解题.
解:(1)由题意得OA=3,OA+OB=AB
∵AB=6OA
∴AB=6![]()
∴OB=AB-OA=18-3=15
∴点B表示的数是![]()
(2)设点P运动x秒,分两种情况:
①当点P在线段OB上时
∵PA=3PB
∴2x+3=3(15-2x)
x=5.25
∴2x=10.5
即点P表示的数是-10.5
②当点P在点B左侧时,得
2x+3=3(2x-15)
x=12
∴2x=24
即点P表示的数是-24.
综上,点P运动5.25秒,此时点P表示的数是-10.5或点P运动12秒,此时点P表示的数是-24.
(3)运动t秒后,PM=3+t-2t=3-t,PN=15+2t-4t=15-2t,MN=18+t-4t=18-3t
当PM=PN时,3-t=15-2t得t=12
当PM=MN时,3-t=18-3t得t=7.5
当PN=MN时,15-2t=18-3t,得t=3


科目:初中数学 来源: 题型:
【题目】学校在“我和我的祖国”快闪拍摄活动中,为学生化妆.其中5名男生和3名女生共需化妆费190元;3名男生的化妆费用与2名女生的化妆费用相同.
(1)求每位男生和女生的化妆费分别为多少元;
(2)如果学校提供的化妆总费用为2000元,根据活动需要至少应有42名女生化妆,那么男生最多有多少人化妆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
科目:初中数学 来源: 题型:
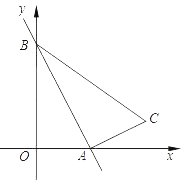
【题目】已知一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC=90°,tan∠ABC=![]() .
.
(1)求点C的坐标;
(2)在第一象限内有一点M(1,m),且点M与点C位于直线AB的同侧,使得2S△ABM=S△ABC,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
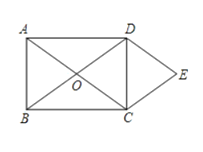
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD
(1)判断四边形OCED是什么特殊四边形?并证明你的结论
(2)当AB、AD满足什么条件时,四边形OCED是正方形?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形AnBnCnDn的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
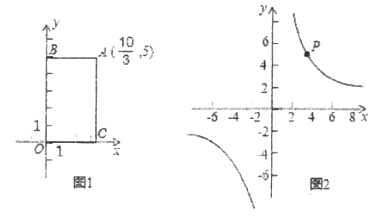
【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长与面积相等,则这个点叫做“和谐点”.
如图1,矩形ABOC的周长与面积相等,则点A是“和谐点”,
(1)点![]() ,其中“和谐点”是_______;
,其中“和谐点”是_______;
(2)如图2,若点![]() 是双曲线
是双曲线![]() 上的“和谐点”,请直接写出所有满足条件的P点坐标__________________________.
上的“和谐点”,请直接写出所有满足条件的P点坐标__________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com