
分析 首先求得关于x的不等式组$\left\{\begin{array}{l}{x-m≤-2}\\{2-x≤2m}\end{array}\right.$无解时,m的取值范围;使函数y=(m-1)x2+2mx+m+2与x轴有交点时,m的取值范围,然后直接利用概率公式求解即可求得答案.
解答 解:∵关于x的不等式组$\left\{\begin{array}{l}{x-m≤-2}\\{2-x≤2m}\end{array}\right.$无解,
∴m-2<2-2m,
解得:m<$\frac{4}{3}$,
∵使函数y=(m-1)x2+2mx+m+2与x轴有交点,
∴△=(2m)2-4(m-1)(m+2)=-4m+8≥0,
∴m≤2且m≠1,
m=1,函数是一次函数与x轴有交点,
综上可得:m<$\frac{4}{3}$,
∴m=-1,0,1,
∴关于x的不等式组$\left\{\begin{array}{l}{x-m≤-2}\\{2-x≤2m}\end{array}\right.$无解,并且使函数y=(m-1)x2+2mx+m+2与x轴有交点的概率为:$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查了概率公式的应用、不等式组无解以及二次函数与x轴的交点问题.用到的知识点为:概率=所求情况数与总情况数之比.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
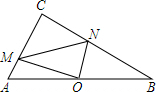 在Rt△ACB中,∠C=90°,点O是AB的中点,点M,N分别在边AC,BC上,OM⊥ON,连MN,AC=4,BC=8,设AM=a,BN=b,MN=c.
在Rt△ACB中,∠C=90°,点O是AB的中点,点M,N分别在边AC,BC上,OM⊥ON,连MN,AC=4,BC=8,设AM=a,BN=b,MN=c.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60° | B. | 60°或120° | C. | 45°或135° | D. | 30°或150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com