
����Ŀ����ͼ����һ�κ�����ϰ�У�A��B���طֱ�ͬʱ�ɳ��ס�������ͧӪ��һ����C����֪B��λ��A�������������84����λ�ã�����Cλ��A����������λ��B�ر�ƫ��48.2�������������ݾ�ȷ����λ��sin48.2���0.7��cos48.2���0.6��tan48.2���1.05��
��1����A��B���طֱ������C�ľ��룻
��2�����ҿ�ͧÿСʱ�ȼ�ͧ����ʻ20���������ͬʱ�ﵽ����Cλ�ã���ס��ҿ�ͧ���ٶȣ�
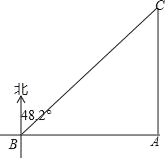
���𰸡���1��A��B���طֱ������C�ľ���Ϊ80���120��������2���ס�������ͧ���ٶȷֱ�Ϊ40����/ʱ��60����/ʱ��
��������
��1����������ó����ǵĶ����������ó�BC�ij������ɵó�AC�ij���
��2�����ͧ���ٶ�Ϊx����/ʱ�����������г���ʽ���̽�ɣ�
�⣺��1�����⣬��Rt��ABC�У���C=48.2��
��sin48.2��=![]() ��tan48.2��=
��tan48.2��=![]()
��BC![]() ��AC
��AC![]()
��A��B���طֱ������C�ľ���Ϊ80���120���
��2�����ͧ���ٶ�Ϊx����/ʱ�����ҿ�ͧ���ٶ�Ϊ��x+20������/ʱ��
��![]()
���x=40
������x=40��ԭ���̵Ľ⣬�������⣬
�𣺼ס�������ͧ���ٶȷֱ�Ϊ40����/ʱ��60����/ʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
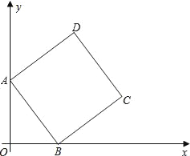
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�DZ߳�Ϊ5�������Σ�����A��y���������ϣ�����B��x���������ϣ�OA��OB�ij�����|OA��4|+��OB��3��2��0��
��1����OA��OB�ij���
��2�����D�����ꣻ
��3����y�����Ƿ���ڵ�P��ʹ��PAB����ABΪ���ĵ��������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��λ���Ͽ������ȣ���ѧ�Աߵ���תת���������������쾰��֮һ���������������ţ���ͼ1������ƽ��ͼ��ͼ2��ʾ���������D����һ̨��DC��CD=0.5�ף����¶�Ϊi=1��0.75����DC�Ϸ���һƽ��BC=1�ף���BC�����MNƽ�У������Ŷ���A����B��ĸ���Ϊ63������AD��MN��Ϊ֪��̨��AB�ij��ȣ������������Ϣ����С�������̨��AB�ij��ȣ�ԼΪ����������ȷ��0.1�ף��ο����ݣ�sin63���0.90��cos63���0.45��tan63���2.00

A. 1.4�� B. 2.5�� C. 2.8�� D. 2.9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽���꼶ѧ��������״�����Ӱ��꼶ѧ���������ȡ����ѧ�����а˰��������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ������������ͳ��ͼ�е���Ϣ�ش������⣺
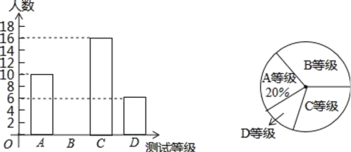
��1�����ε�����ȡ���� ���ĵ��鷽ʽ���������ղ�������������������
��2�����ε��鹲������________�ˣ�ͼ��2����ѡ��C��Բ�Ľ�Ϊ ______�ȣ�
��3���β��Խ��ΪB�ȼ���ѧ����������ȫ����ͳ��ͼ��
��4��������ѧ���꼶����900��ѧ����������ư��꼶ѧ�������ܲ��Խ��ΪD�ȼ���ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ں���l������ֱ��й۲��A��B����B������l�ľ���BDΪ4km����Aλ�ڵ�B��ƫ��60�㷽������B���20km��������һ���ִ���λ�ڵ�A��ƫ��74�㷽���C�����ظú����Զ������������۲��A�����Ϸ���E�����������ִ��ĺ���·��CE�ij��ȣ��������ȷ��0.1km�����ο����ݣ�![]() ��1.73��sin74���0.96��cos74���0.28��tan74���3.49��
��1.73��sin74���0.96��cos74���0.28��tan74���3.49��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨����a��b֮���һ�����㣬������a��b�������ac��b����ô��a��b����c�����磺��Ϊ23��8�����ԣ�2��8����3��
��1�����������涨����գ���3��81������ ��������![]() ����
����![]() ������ ������2����2��256�������� ����
������ ������2����2��256�������� ����
��2������3��4��+��3��6������3��x������x��ֵ��
��3��֤������2��3��+��2��5������8��3375����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ���涨���ѵ�
���涨���ѵ�![]() ��������
��������![]() ��Գƣ�������ƽ��1����λ��Ϊһ�α仯��������һ�α任��
��Գƣ�������ƽ��1����λ��Ϊһ�α仯��������һ�α任��![]() ������Ϊ_______�������ڶ��α任��
������Ϊ_______�������ڶ��α任��![]() ������Ϊ_____����ô��������2019�α任��
������Ϊ_____����ô��������2019�α任��![]() ������Ϊ_______��
������Ϊ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����x�ύ�ڵ�A����1��0������y�ύ�ڵ�B���ҶԳ���Ϊx=1����������ĸ����ۣ�
�ٵ�x����1ʱ��y��0��
��һԪ���η���ax2+bx+c=0������Ϊx1=��1��x2=3��
�۵�y��0ʱ��x����1��
�������������㣨x1��y1������x2��y2������x1��x2��2ʱ��y1��y2
������ȷ���۵ĸ����ǣ�������

A. 3 B. 2 C. 1 D. 0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��壺���һ��������һ�����ϵĸߵ��������ߣ���ô��������ν������ȸߵ��������Σ������߽�����������ε����ȵ�����

��1���������⣺
��ͼ1������ABC�У�AC=6��BC=3����ACB=30�������ж���ABC�Ƿ������ȸߵ��������Σ���˵�����ɣ�
��2������̽����
��ͼ2����ABC�����ȸߵ��������Σ�BC�����ȵ���������ABC����BC����ֱ�ߵĶԳ�ͼ�εõ���A'BC������AA����ֱ��BC�ڵ�D������B����AA��C�����ģ���![]() ��ֵ��
��ֵ��
��3��Ӧ����չ��
��ͼ3����֪l1��l2��l1��l2֮��ľ���Ϊ2�����ȸߵ�����ABC�����ȵ���BC��ֱ��l1�ϣ���A��ֱ��l2�ϣ���һ�ߵij���BC��![]() ��������ABC�Ƶ�C��˳ʱ�뷽����ת45���õ���A'B'C��A��C����ֱ�߽�l2�ڵ�D����CD��ֵ��
��������ABC�Ƶ�C��˳ʱ�뷽����ת45���õ���A'B'C��A��C����ֱ�߽�l2�ڵ�D����CD��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com