
【题目】如图,在平面直角坐标系中,四边形ABCD是边长为5的正方形,顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA,OB的长满足|OA﹣4|+(OB﹣3)2=0.
(1)求OA,OB的长;
(2)求点D的坐标;
(3)在y轴上是否存在点P,使△PAB是以AB为腰的等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
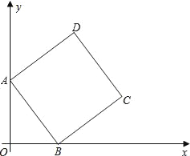
【答案】(1)OA=4,OB=3.(2)点D坐标为(4,7).(3)当PA=AB=5时,P(0,9)或(0,﹣1),当PB=BA时,P(0,﹣4).
【解析】
(1)利用非负数的性质即可解决问题.
(2)如图2中,作DE⊥y轴于E.证明△AOB≌△DEA(AAS),推出DE=OA=4,AE=OB=3,即可解决问题.
(3)分两种情形分别求解即可解决问题.
解:(1)∵|OA﹣4|+(OB﹣3)2=0,
又∵|OA﹣4|≥0,(OB﹣3)2≥0,
∴OA=4,OB=3.
(2)如图2中,作DE⊥y轴于E.

∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAE+∠BAO=90°,∠DAE+∠ADE=90°,
∴∠BAO=∠ADE,
∵∠DEA=∠AOB=90°,
∴△AOB≌△DEA(AAS),
∴DE=OA=4,AE=OB=3,
∴OE=7,
∴点D坐标为(4,7).
(3)存在.在Rt△AOB中,AB=![]() =5,
=5,
∴当PA=AB=5时,P(0,9)或(0,﹣1),
当PB=BA时,P(0,﹣4).


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
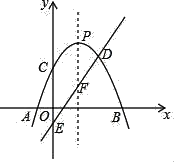
【题目】如图,抛物线L:y=﹣(x﹣2)2+m2+2m与x轴交于A,B,直线y=kx﹣1与y轴交于E,与L的对称轴交于点F(n,3),与L交于D,抛物线L的对称轴与L交于P.
(1)求k的值.
(2)点P能否与点F关于x轴的对称点重合?若认为能,请求出m的值;若认为不能,说明理由.
(3)小林研究了抛物线L的解析式后,得到了如下的结论:因为m可以取任意实数,所以点C可以在y轴上任意移动,即C点可以到达y轴的任何位置,你认为他说的有道理吗?说说你的想法.
(4)当抛物线L与直线y=kx﹣1有两个公共点时,直接写出适合条件的m的最大整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
(1)若A(4,n)和B(n+![]() ,3),求反比例函数的表达式;
,3),求反比例函数的表达式;
(2)若m=1,
①当x2=1时,直接写出y1的取值范围;
②当x1<x2<0,p=![]() ,q=
,q=![]() ,试判断p,q的大小关系,并说明理由;
,试判断p,q的大小关系,并说明理由;
(3)若过A、B两点的直线y=x+2与y轴交于点C,连接BO,记△COB的面积为S,当![]() <S<1,求m的取值范围.
<S<1,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
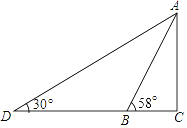
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
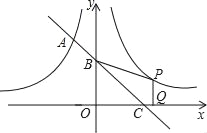
【题目】如图,一次函数的图象与反比例函数![]() 的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<﹣1时,一次函数值大于反比例函数值,当x>﹣1时,一次函数值小于反比例函数值.
的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<﹣1时,一次函数值大于反比例函数值,当x>﹣1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数y2=![]() 的图象与
的图象与![]() 的图象关于y轴对称,在y2=
的图象关于y轴对称,在y2=![]() 的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q、R处,且相距30海里.如果知道“远航”号沿东北方向航行,则“海天”号沿( )方向航行.

A.西南B.东北C.西北D.东南
查看答案和解析>>
科目:初中数学 来源: 题型:
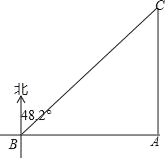
【题目】如图,在一次海警演习中,A、B两地分别同时派出甲、乙两快艇营救一货轮C,已知B地位于A地正西方向相距84海里位置,货轮C位于A地正北方向,位于B地北偏东48.2°方向(所有数据精确到个位,sin48.2°≈0.7,cos48.2°≈0.6,tan48.2°≈1.05)
(1)求A、B两地分别与货轮C的距离;
(2)若乙快艇每小时比甲快艇多行驶20海里,且它们同时达到货轮C位置,求甲、乙快艇的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com