
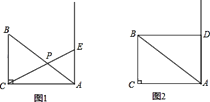
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯACB=90ЁуЃЌBC=6ЃЌAC=8ЃЎЕуEгыЕуBдкACЕФЭЌВрЃЌЧвAEЁЭACЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕуEВЛгыЕуAжиКЯЃЌСЌНсCEНЛABгкЕуPЃЎЩшAE=xЃЌAP=yЃЌЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЕуEЃЌЪЙЁїPAEгыЁїABCЯрЫЦЃЌШєДцдкЃЌЧѓAEЕФГЄЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
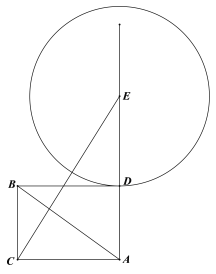
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуBзїBDЁЭAEЃЌДЙзуЮЊDЃЎНЋвдЕуEЮЊдВаФЃЌEDЮЊАыОЖЕФдВМЧЮЊЁбEЃЎШєЕуCЕНЁбEЩЯЕуЕФОрРыЕФзюаЁжЕЮЊ8ЃЌЧѓЁбEЕФАыОЖЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ9Лђ
ЃЛЃЈ3ЃЉ9Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЙДЙЩЖЈРэЧѓГіABЕФГЄЃЌдйИљОнЁїAPEЁзЁїBPCЕУГіБШР§ЪНЃЌећРэМДПЩЧѓГіНсЙћЃЛ
ЃЈ2ЃЉЯШХаЖЯжЛгаЁЯEPA=90ЁуЪБЃЌПЩЪЙЁїPAEгыЁїABCЯрЫЦЃЌдйжЄУїЁїABCЁзЁїEACЃЌНјвЛВНИљОнЯрЫЦШ§НЧаЮЕФаджЪМДПЩЧѓГіНсЙћЃЛ
ЃЈ3ЃЉЯШгЩЬтвтХаЖЯЕуCБидкЁбEЭтВПЃЌгкЪЧЕуCЕНЁбEЩЯЕуЕФОрРыЕФзюаЁжЕЮЊCEЉDEЃЌдйЗжЕуEдкЯпЖЮADЩЯКЭЯпЖЮADЕФбгГЄЯпЩЯСНжжЧщПіЃЌдкЁїAECжаИљОнЙДЙЩЖЈРэСаГіЗНГЬЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉЁпAEЁЭACЃЌЁЯACB=90ЁуЃЌ
ЁрAEЁЮBCЃЌ
ЁрЁїAPEЁзЁїBPCЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпBC=6ЃЌAC=8ЃЌ
ЁрAB=![]() =10ЃЌ
=10ЃЌ
ЁпAE=xЃЌAP=yЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпЁЯACB=90ЁуЃЌЖјЁЯPAEгыЁЯPEAЖМЪЧШёНЧЃЌ
ЁрвЊЪЙЁїPAEгыЁїABCЯрЫЦЃЌжЛгаЁЯEPA=90ЁуЃЌМДCEЁЭABЃЌ
ДЫЪБЁїABCЁзЁїECAЃЌдђ![]() ЃЌЁрAE=
ЃЌЁрAE=![]() ЃЎ
ЃЎ
ЙЪДцдкЕуEЃЌЪЙЁїABCЁзЁїEAPЃЌДЫЪБAE=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩЬтвтПЩжЊЕуCБидкЁбEЭтВПЃЌДЫЪБЕуCЕНЁбEЩЯЕуЕФОрРыЕФзюаЁжЕЮЊCEЉDEЃЎ
ЩшAE=xЃЎЂйЕБЕуEдкЯпЖЮADЩЯЪБЃЌШчЭМЃЌED=6ЉxЃЌEC=6Љx+8=14ЉxЃЌ
дђдкRtЁїAECжаЃЌИљОнЙДЙЩЖЈРэЃЌЕУx2+82=ЃЈ14ЉxЃЉ2ЃЌНтЕУЃКx=![]() ЃЌ
ЃЌ
МДЁбEЕФАыОЖЮЊ![]() ЃЎ
ЃЎ
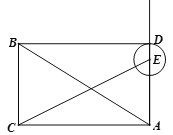
ЂкЕБЕуEдкЯпЖЮADбгГЄЯпЩЯЪБЃЌШчЭМЃЌED=xЉ6ЃЌEC=xЉ6+8=x+2ЃЌ
дђдкRtЁїAECжаЃЌИљОнЙДЙЩЖЈРэЃЌЕУx2+82=ЃЈx+2ЃЉ2ЃЌНтЕУЃКx=15ЃЌМДЁбEЕФАыОЖЮЊ9ЃЎ
ЁрЁбEЕФАыОЖЮЊ9Лђ![]() ЃЎ
ЃЎ


 ИпжаБиЫЂЬтЯЕСаД№АИ
ИпжаБиЫЂЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁѕABCDжаЃЌABЁЭACЃЌABЃН1ЃЌBCЃН![]() ЃЎЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌНЋжБЯпACШЦЕуOЫГЪБеыа§зЊЃЌЗжБ№НЛBCЃЌADгкЕуEЃЌFЃЎ
ЃЎЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌНЋжБЯпACШЦЕуOЫГЪБеыа§зЊЃЌЗжБ№НЛBCЃЌADгкЕуEЃЌFЃЎ
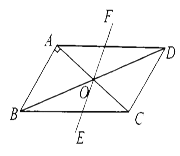
(1)ЪдЫЕУїдка§зЊЙ§ГЬжаЃЌЯпЖЮAFгыECзмБЃГжЯрЕШЃЛ
(2)дка§зЊЙ§ГЬжаЃЌЫФБпаЮBEDFПЩФмЪЧСтаЮТ№?ШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЛШчЙћФмЃЌЧыжБНгаДГіДЫЪБACШЦЕуOЫГЪБеыа§зЊЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=8ЃЌAC=6ЃЎЕуDдкБпABЩЯЃЌAD=4.5ЃЎЁїABCЕФНЧЦНЗжЯпAEНЛCDгкЕуFЃЎ
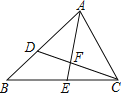
ЃЈ1ЃЉЧѓжЄЃКЁїACDЁзЁїABCЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШЅФъЕФДДНЈШЋЙњЮФУїГЧЪаЛюЖЏжаЃЌБЇзХЮвЮЊЮФУїШ№АВГівЛЗнСІЕФЯыЗЈЃЌаЁЛЊОЭЙЋжкЖддкВЭЬќЮќбЬЕФЬЌЖШНјааСЫЫцЛњГщбљЕїВщЃЌжївЊгаЫФжжЬЌЖШЃКAЁЂЙЫПЭГіУцжЦжЙЃЛBЁЂШАЫЕНјЮќбЬЪвЃЛCЁЂВЭЬќРЯАхГіУцжЦжЙЃЛDЁЂЮоЫљЮНЃЎЫћНЋЕїВщНсЙћЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыФуИљОнЭМжаЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉетДЮГщбљЕФЙЋжкга__________ШЫЃЛ
ЃЈ2ЃЉЧыНЋЭГМЦЭМЂйВЙГфЭъећЃЛ
ЃЈ3ЃЉдкЭГМЦЭМЂкжаЃЌЁАЮоЫљЮНЁБВПЗжЫљЖдгІЕФдВаФНЧЪЧЖрЩйЖШЃП
ЃЈ4ЃЉШєШ№АВШЋЪаШЫПкга120ЭђШЫЃЌЙРМЦдоГЩЁАВЭЬќРЯАхГіУцжЦжЙЁБЕФгаЖрЩйЭђШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
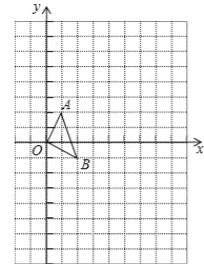
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮЭјИёжаЃЌУПвЛИіаЁе§ЗНаЮЕФБпГЄЖМЮЊ1ЃЌЁїOABЕФЖЅЕуЗжБ№ЮЊOЃЈ0ЃЌ0ЃЉЃЌAЃЈ1ЃЌ2ЃЉЃЌBЃЈ2ЃЌЉ1ЃЉЃЎ
ЃЈ1ЃЉвдЕуOЃЈ0ЃЌ0ЃЉЮЊЮЛЫЦжааФЃЌАДЮЛЫЦБШ1ЃК3дкЮЛЫЦжааФЕФЭЌВрНЋЁїOABЗХДѓЮЊЁїOAЁфBЁфЃЌЗХДѓКѓЕуAЁЂBЕФЖдгІЕуЗжБ№ЮЊAЁфЁЂBЁфЃЌЧыдкЭМжаЛГіЁїOAЁфBЁфЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉжаЃЌШєCЃЈaЃЌbЃЉЮЊЯпЖЮABЩЯШЮвЛЕуЃЌаДГіБфЛЏКѓЕуCЕФЖдгІЕуC'ЕФзјБъ____ЃЛ
ЃЈ3ЃЉжБНгаДГіЫФБпаЮABAЁфBЁфЕФУцЛ§ЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ ЁїABC ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ A(-2,3)ЁЂB(-6,0)ЁЂC(-1,0).
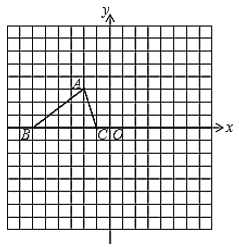
ЃЈ1ЃЉНЋЁїABCШЦзјБъдЕуOФцЪБеыа§зЊ 90Ёу. ЛГіЭМаЮЃЌжБНгаДГіЕуBЕФЖдгІЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧыжБНгаДГіЃКвд AЁЂBЁЂC ЮЊЖЅЕуЕФЦНааЫФБпаЮЕФЕкЫФИіЖЅЕу D ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2ЃЋbxЃЋc(aЁй0)ЕФЭМЯѓШчЭМЫљЪОЃЌИљОнЭМЯѓНтД№ЯТСаЮЪЬтЃЎ
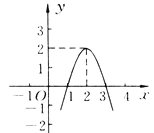
(1)аДГіЗНГЬax2ЃЋbxЃЋcЃН0ЕФСНИіИљЃЛ
(2)аДГіВЛЕШЪНax2ЃЋbxЃЋcЃО0ЕФНтМЏЃЛ
(3)аДГіyЫцxЕФдіДѓЖјМѕаЁЕФздБфСПxЕФШЁжЕЗЖЮЇЃЛ
(4)ШєЗНГЬax2ЃЋbxЃЋcЃНkгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮїФўНЬг§ОждкОжЪєИїГѕжабЇаЃЩшСЂЁАзджїбЇЯАШеЁБ.ЙцЖЈУПжмШ§бЇаЃВЛЕУвдШЮКЮаЮЪНВМжУМвЭЅзївЕЃЌЮЊСЫНтИїбЇаЃЕФТфЪЕЧщПіЃЌДгЦпЁЂАЫФъМЖбЇЩњжаЫцЛњГщШЁСЫВПЗжбЇЩњЕФЗДРЁБэ.еыЖдвдЯТСљИіЯюФПЃЈУПШЫжЛФмбЁвЛЯюЃЉЃК![]() .ПЮЭтдФЖСЃЛ
.ПЮЭтдФЖСЃЛ![]() .МвЮёРЭЖЏЃЛ
.МвЮёРЭЖЏЃЛ![]() .Ьхг§ЖЭСЖЃЛ
.Ьхг§ЖЭСЖЃЛ![]() .бЇПЦбЇЯАЃЛ
.бЇПЦбЇЯАЃЛ![]() .ЩчЛсЪЕМљЃЛ
.ЩчЛсЪЕМљЃЛ![]() .ЦфЫћЯюФПНјааЕїВщ.ИљОнЕїВщНсЙћЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
.ЦфЫћЯюФПНјааЕїВщ.ИљОнЕїВщНсЙћЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
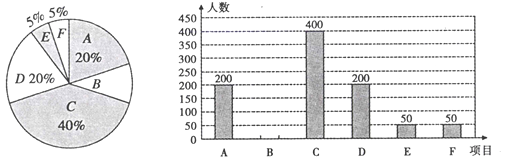
ЃЈ1ЃЉДЫДЮГщВщЕФбљБОШнСПЮЊ____________ЃЌЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉШЋЪадМга4ЭђУћдкаЃГѕжабЇЩњЃЌЪдЙРМЦШЋЪабЇЩњжабЁдёЬхг§ЖЭСЖЕФШЫЪ§дМгаЖрЩйШЫЃП
ЃЈ3ЃЉЦпФъМЖЃЈ1ЃЉАрДгбЁдёЩчЛсЪЕМљЕФ2УћХЎЩњКЭ1УћФаЩњжабЁХЩ2УћВЮМгаЃМЖЩчЛсЪЕМљЛюЖЏ.ЧыФугУЪїзДЭМЛђСаБэЗЈЧѓГіЧЁКУбЁЕН1Фа1ХЎЕФИХТЪЪЧЖрЩйЃПВЂСаОйГіЫљгаЕШПЩФмЕФНсЙћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЃЌгаЯТСа4ИіНсТлЃКЂйabcЃО0ЃЛЂкbЃОa+cЃЛЂл4a+2b+cЃО0ЃЛЂмb2-4acЃО0ЃЛЦфжае§ШЗЕФИіЪ§гаЃЈ ЃЉ
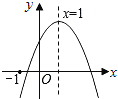
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com