
【题目】直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 为⊙
为⊙![]() 的直径,动点
的直径,动点![]() 沿
沿![]() 方向从点
方向从点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,动点
的速度运动,动点![]() 沿
沿![]() 方向从点
方向从点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,当其中一点停止时,另一点也随之停止运动.
两点同时出发,当其中一点停止时,另一点也随之停止运动.

(![]() )求⊙
)求⊙![]() 的直径.
的直径.
(![]() )当
)当![]() 为何值时,四边形
为何值时,四边形为等腰梯形?
(![]() )是否存在某一时刻
)是否存在某一时刻![]() ,使直线
,使直线![]() 与⊙
与⊙![]() 相切?若存在,求出
相切?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
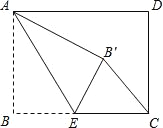
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷饭后出去散步,从家中走20分钟到离家900米的公园,与朋友聊天10分钟后,用15分钟返回家中.下面图形表示王大爷离时间x(分)与离家距离y(米)之间的关系是( )
A.  B.
B. 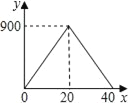
C. 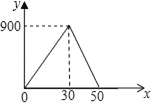 D.
D. 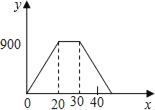
查看答案和解析>>
科目:初中数学 来源: 题型:
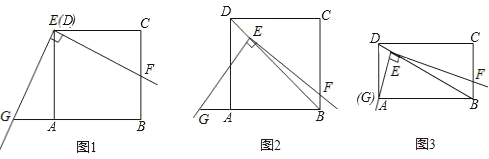
【题目】请你认真阅读下面的小探究系列,完成所提出的问题.
(1)如图1,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F,将另一边交BA的延长线于点G.求证:EF=EG.
(2)如图2,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF EG(用“=”或“≠”填空)
(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,BC=3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,三角形
,三角形![]() 是三角形
是三角形![]() 经过平移得到的图形,设点
经过平移得到的图形,设点![]() 是三角形
是三角形![]() 中的任意一点,其平移后的对应点为
中的任意一点,其平移后的对应点为![]() .
.
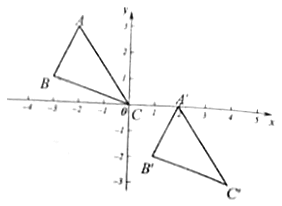
![]() 请写出三角形
请写出三角形![]() 平移到三角形
平移到三角形![]() 的过程;
的过程;
![]() 分别写出点
分别写出点![]() 的坐标;
的坐标;
![]() 求
求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市煤气公司准备给某新建小区的用户安装管道煤气,现有![]() 用户提出了安装申请,此外每天还有新的用户提出申请,假设煤气公司每个安装小组安装的数量相同,且每天申请安装的用户数也相同,若煤气公司安排
用户提出了安装申请,此外每天还有新的用户提出申请,假设煤气公司每个安装小组安装的数量相同,且每天申请安装的用户数也相同,若煤气公司安排![]() 个安装小组同时做,则
个安装小组同时做,则![]() 天就可以装完所有新、旧用户的申请;若煤气公司安排
天就可以装完所有新、旧用户的申请;若煤气公司安排![]() 个安装小组同时做,则
个安装小组同时做,则![]() 天可以装完所有新旧用户的申请.
天可以装完所有新旧用户的申请.
![]() 求每天新申请安装的用户数及每个安装小组每天安装的数量;
求每天新申请安装的用户数及每个安装小组每天安装的数量;
![]() 如果要求在
如果要求在![]() 天内安装完所有新、旧用户的申请,但前
天内安装完所有新、旧用户的申请,但前![]() 天煤气公司只能派出
天煤气公司只能派出![]() 个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.
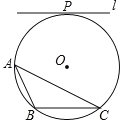
(1)仅用无刻度的直尺,画出一条弦,使这条炫将△ABC分成面积相等的两部分(保留作图痕迹,不写画法).
(2)求弦BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
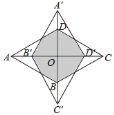
【题目】如图,菱形ABCD的一个内角是60,将它绕对角线的交点O顺时针旋转90后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为![]() ,则菱形ABCD的边长为_________.
,则菱形ABCD的边长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com