
【题目】如图,二次函数的图象与x轴交于A、B两点,与y轴交于点C,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)求D点的坐标;
(2)求一次函数及二次函数的解析式;
(3)求抛物线的顶点坐标和对称轴;
(4)根据图象写出使一次函数值大于二次函数的值的x的取值范围.
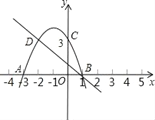
【答案】(1) (﹣2,3);(2) y=﹣x+1;y=﹣x2﹣2x+3;(3)顶点坐标(﹣1,4),对称轴为直线x=﹣1;(4)x<-2或x>1
【解析】
(1)根据函数图象求出对称轴,再根据二次函数的对称性写出点D的坐标即可;
(2)分别利用待定系数法求函数解析式解答;
(3)把抛物线解析式整理成顶点式形式,然后写出即可;
(4)根据图象写出一次函数图象在二次函数图象上方部分的x的取值范围即可.
解:(1)由图可知,二次函数图象的对称轴为直线x=﹣1,
∵点C、D是二次函数图象上的一对对称点,
∴点D的坐标为(﹣2,3);
(2)设直线BD的解析式为y=kx+b(k≠0),
则![]() ,
,
解得![]() ,
,
所以,直线BD的解析式为y=﹣x+1;
设二次函数的解析式为y=ax2+bx+c,
则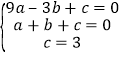 ,
,
解得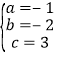 ,
,
所以,二次函数的解析式为y=﹣x2﹣2x+3;
(3)∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的顶点坐标为(﹣1,4),
对称轴为直线x=﹣1,
(4)根据图象写出一次函数图象在二次函数图象上方部分即可得x<-2或x>1.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(边框线加粗画出,并涂上阴影)

(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
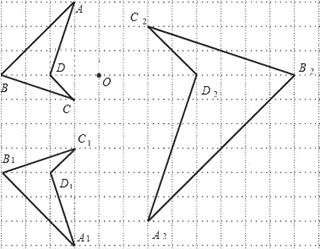
(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M、N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少(注:只要写出对应边的比即可);
(3)求图形A2B2C2D2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
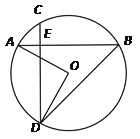
【题目】如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
(1)求证:EB=ED.
(2)若AO=6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列函数:(1)y=3﹣2x2;(2)y=![]() ;(3)y=3x(2x﹣1);(4)y=﹣2
;(3)y=3x(2x﹣1);(4)y=﹣2![]() x2;(5)y=x2﹣(3+x)2;(6)y=mx2+nx+p(其中m、n、p为常数).其中一定是二次函数的有( )
x2;(5)y=x2﹣(3+x)2;(6)y=mx2+nx+p(其中m、n、p为常数).其中一定是二次函数的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
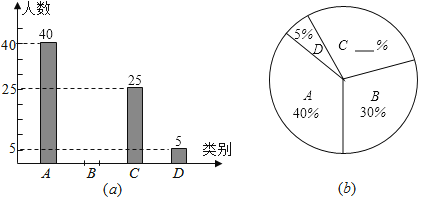
【题目】为了了解某区2018年初中毕业生毕业后的去向,某区教育部门对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中;C,直接进入社会就业;D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问:
(1)此次共调查了多少名初中毕业生?
(2)将两幅统计图中不完整的部分补充完整;
(3)若某区2018年初三毕业生共有3500人,请估计2019年初三毕业生中读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
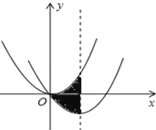
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )
A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记
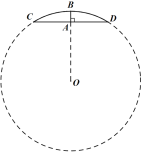
载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①)
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.再次阅读后,发现AB=______寸,CD=____寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
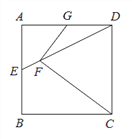
【题目】己知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF=CD,过点F作FG⊥FC交AD于点G.
(1)求证:GF=GD;
(2)联结AF,求证:AF⊥DE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com