
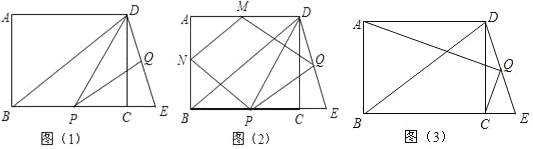
����Ŀ���ھ���ABCD�У�AB��6��BC��8����EΪBC�ӳ�����һ�㣬��BD��BE������DE��QΪDE���е㣬��һ����P��B���������BC��ÿ��1����λ���ٶ���E���˶����˶�ʱ��Ϊt�룮
(1)��ͼ1������DP��PQ����S��DPQ��_____(�ú�t��ʽ�ӱ�ʾ)��
(2)��ͼ2��M��N�ֱ�ΪAB��AD���е㣬��tΪ��ֵʱ���ı���MNQPΪƽ���ı��Σ���˵�����ɣ�
(3)��ͼ3������CQ��AQ�����ж�AQ��CQ��λ�ù�ϵ������֤����
���𰸡�(1)15��![]() t��(2)t��5ʱ���ı���MNQPΪƽ���ı��Σ�(3)AQ��CQ.
t��(2)t��5ʱ���ı���MNQPΪƽ���ı��Σ�(3)AQ��CQ.
��������
(1)�ɹ��ɶ�������BD��10���������ε������ʽ��S��DPQ��![]() (S��BED��S��BDP)����⣻
(S��BED��S��BDP)����⣻
(2)��t��5ʱ���ɵ�BP��5��![]() BE������λ�߶����ɵ�MN��BD��MN��
BE������λ�߶����ɵ�MN��BD��MN��![]() BD��5��PQ��BD��PQ��
BD��5��PQ��BD��PQ��![]() BD��5���ɵ�MN��PQ��MN��PQ���ɵý��ۣ�
BD��5���ɵ�MN��PQ��MN��PQ���ɵý��ۣ�
(3)����BQ���ɵ��������ε����ʿɵá�AQD+��BQA��90������ֱ�������ε����ʿɵ�DQ��CQ����DCQ����CDQ������SAS����֤��ADQ�ա�BCQ���ɵá�AQD����BQC�����ɵý��ۣ�
�⣺(1)���ı���ABCD�Ǿ��Σ�AB��6��BC��8��
��BC��8��CD��6��
��BD��![]() ��10
��10
��BD��BE��10
��QΪDE���е㣬
��S��DPQ��![]() S��DPE��
S��DPE��
��S��DPQ��![]() (S��BED��S��BDP)��
(S��BED��S��BDP)��![]() ,
,
�ʴ�Ϊ15��![]() t
t
(2)��t��5ʱ���ı���MNQPΪƽ���ı��Σ�
�������£���M��N�ֱ�ΪAB��AD���е㣬
��MN��BD��MN��![]() BD��5��
BD��5��
��t��5ʱ��
��BP��5��![]() BE���ҵ�Q��DE���е㣬
BE���ҵ�Q��DE���е㣬
��PQ��BD��PQ��BD��5
��MN��PQ��MN��PQ
���ı���MNQP��ƽ���ı���
(3)AQ��CQ
�������£���ͼ������BQ��
��BD��BE����Q��DE�е㣬
��BQ��DE��
���AQD+��BQA��90��
����Rt��DCE�У���Q��DE�е㣬
��DQ��CQ��
���DCQ����CDQ���ҡ�ADC����BCD��90��
���ADQ����BCQ����BC��AD��DQ��CQ
���ADQ�ա�BCQ(SAS)
���AQD����BQC���ҡ��AQD+��BQA��90��
���BQC+��BQA��90��
���AQC��90��
��AQ��CQ


 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݹ���ʵ�еġ�����ѧ�����ʽ����������Ի�������һѧ�����߽��г������飬�Ա��ܽỳ������һѧ���ִ���������⣬������Ӱ�����أ�Ϊѧ���Ľ�����չ��ѧУ���������ĸ�����������.��֪��������һѧ��������840�ˣ�Ů��800�ˣ����ǵ�������![]() ��Χ�ڣ������ȡ��һѧ�����г������顣��ȡ�������У�������Ů����2�ˣ������������ݻ�������ͳ��ͼ����
��Χ�ڣ������ȡ��һѧ�����г������顣��ȡ�������У�������Ů����2�ˣ������������ݻ�������ͳ��ͼ����


����ͳ��ͼ���ṩ����Ϣ������˵����
�ٳ�ȡ�����������У�����![]() ֮���ѧ����18�ˣ�
֮���ѧ����18�ˣ�
�ڳ�һѧ����Ů�������ߵ���λ����![]() �飻
�飻
�۳�ȡ�������г�ȡŮ��������������38��
�ܳ�һѧ��������![]() ֮���ѧ��Լ��800�ˡ����к������ǣ� ��
֮���ѧ��Լ��800�ˡ����к������ǣ� ��
A. �٢�B. �٢�C. �ڢ�D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��ˮ����ס������ص�ˮ�����м���ˮ
��ˮ����ס������ص�ˮ�����м���ˮ![]() ��֣��ҵ���ˮ
��֣��ҵ���ˮ![]() ��֣�
��֣�![]() ��ˮ����ɵ���ˮ
��ˮ����ɵ���ˮ![]() ��֣���
��֣���![]() ˮ���
ˮ���![]() ǧ�ף����ҵ�
ǧ�ף����ҵ�![]() ǧ��;��
ǧ��;��![]() ˮ���
ˮ���![]() ǧ�ף����ҵ�
ǧ�ף����ҵ�![]() ǧ�ף����һ�����˷���ʹˮ�ĵ�������(��λ:���ǧ��)�����ܴ�
ǧ�ף����һ�����˷���ʹˮ�ĵ�������(��λ:���ǧ��)�����ܴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ա߳�Ϊ![]() �������ε�����
�������ε�����![]() Ϊ�˵㣬���������ֱ�����ߣ��ֱ��������εı߽���
Ϊ�˵㣬���������ֱ�����ߣ��ֱ��������εı߽���![]() ��
��![]() ���㣬���߶�
���㣬���߶�![]() ��ȡֵ��Χ��________��
��ȡֵ��Χ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��M����ABC�ı�BC���е㣬ANƽ����BAC��BN��AN�ڵ�N���ӳ�BN��AC�ڵ�D����֪AB=10��BC=15��MN=3

��1����֤��BN=DN��
��2������ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˲μ�ij������Ŀѵ����Ϊ�˱����о��������5�ε�ѵ���ɼ��ֱ���ʵ�ߺ�����������������ͼ������Ľ��۴�����ǣ�������

A. �ҵĵ�2�γɼ����5�γɼ���ͬ
B. ��3�β��ԣ��ijɼ����ҵijɼ���ͬ
C. ��4�β��ԣ��ijɼ����ҵijɼ���2��
D. ��5�β����У��ijɼ������ҵijɼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
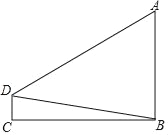
����Ŀ����ͼ�������������ˮƽ����BCΪ40m����D����A�������Ϊ30�㣬B��ĸ���Ϊ10����������AB�ĸ߶ȣ��������С�����һλ����
�ο�����sin10���0.17��cos10���0.98��tan10���0.18��![]() ȡ1.732��
ȡ1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ת����8�����ε���������,����ת��ת��1��,��ת��ֹͣת��ʱ,���������¼������Ŀ����ԵĴ�С,������Щ�¼�����Ű������Ŀ����Դ�С�����˳���ų�һ����__________��������ţ�

��1��ָ�����ڱ���3�������ڣ���2��ָ�����ڱ���9�������ڣ�
��3��ָ�����ڱ������ֵ������ڣ���4��ָ�����ڱ���������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
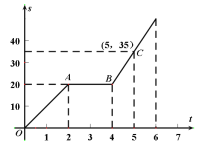
����Ŀ��С�������г��Ӽص��ҵأ�ͼ�е����߱�ʾС����ʻ��·��![]() ������ʱ��
������ʱ��![]() ֮��ĺ�����ϵ���Ը��ݺ���ͼ�����������⣺
֮��ĺ�����ϵ���Ը��ݺ���ͼ�����������⣺
��1��С����;��ͣ����____![]() ��С����ͣ��֮ǰ���ٶ�Ϊ____
��С����ͣ��֮ǰ���ٶ�Ϊ____![]() ��
��
��2�����߶�![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��3��С������1Сʱ��С��Ҳ�Ӽ�����ͬ·���������ҵ����У�![]()
![]() ʱ������ͬʱ�����ҵأ���
ʱ������ͬʱ�����ҵأ���![]() Ϊ��ֵʱ��������;��������
Ϊ��ֵʱ��������;��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com