
【题目】中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了40名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择),请根据统计图完成下列问题:
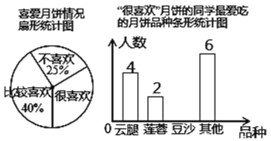
(1)被调查的40名同学中,“很喜欢”;月饼的学生有 人;条形统计图中,喜欢“豆沙”月饼的学生有 人;并补全条形统计图;
(2)若该校共有学生800人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有 人.
(3)甲同学最爱吃云腿月饼,现有重量、包装完全一样的云腿(A)、豆沙(B)、莲蓉(C)、蛋黄(D)四种月饼各一个,让甲任意选两个,请用画树状图法或列表法,求出甲选中的月饼都不是他最爱吃的云腿月饼(A)的概率.
【答案】(1)14,2,见解析;(2)600;(3)树状图见解析,![]()
【解析】
(1)用40乘以“很喜欢”月饼的百分比,再用算出来的人数减去最爱吃云腿、莲蓉和其他品种的人数即可得到结果;
(2)分别算出“很喜欢”的和“比较喜欢”的人数,再相加即可;
(3)画出树状图,根据概率的定义即可解决.
解:(1)40×(1-25%-40%)=14人,
14-4-2-6=2人,
补全统计图如下:

(2)800名学生中“很喜欢”的有800×35%=280人,
800名学生中“比较喜欢”的有800×40%=320人,
∴估计该校学生中“很喜欢”和“比较喜欢”月饼的共有600人.
故答案为:600;
(3)由题意可得:
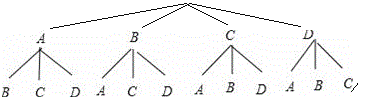
共有12种等可能情况,其中选中的月饼都不是云腿的有6种情况,
∴P(选中的月饼都不是云腿)![]()


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与一直线相交于
与一直线相交于![]() ,
,![]() 两点.
两点.
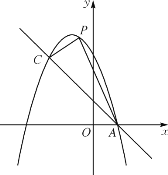
(1)求抛物线的函数表达式;
(2)求直线![]() 的函数表达式;
的函数表达式;
(3)若![]() 是抛物线上位于直线
是抛物线上位于直线![]() 上方的一个动点,求
上方的一个动点,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两直角边比为1:2的直角三角形叫做和合三角形.
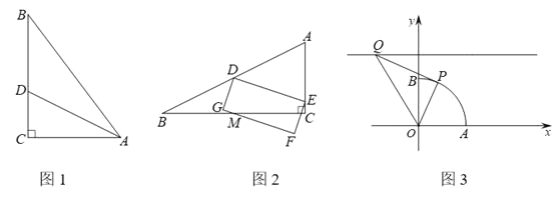
(1)如图1,△ABC中,∠C= ![]() ,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
(2)如图2,和合△ABC中,∠C= ![]() ,AC=
,AC= ![]() ,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
(3)如图3,扇形OAB中,∠AOB= ![]() ,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是
,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是 ![]() 一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有【 】

A.1组 B.2组 C.3组 D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
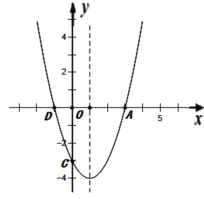
【题目】如图,已知抛物线![]() 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为
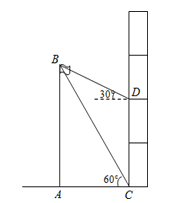
A.9米B.6![]() 米C.6米D.(6+
米C.6米D.(6+![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,将这些学生的测试成绩(x)分为四个等级:优秀![]() ;良好
;良好![]() ;及格
;及格![]() ;不及格
;不及格![]() ,并绘制成以下两幅统计图.
,并绘制成以下两幅统计图.
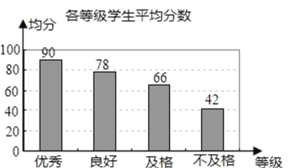
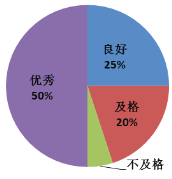
根据以上信息,解答下列问题:
(1)在抽取的学生中不及格人数所占的百分比是______;
(2)计算所抽取学生测试成绩的平均分;
(3)若不及格学生的人数为2人,请估算出该校九年级学生中优秀等级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 的顶点是A(1,3),将OA绕点O逆时针旋转
的顶点是A(1,3),将OA绕点O逆时针旋转![]() 后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.
后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.

(1)求抛物线的解析式;
(2)P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与![]() 的边分别交于M,N两点,将
的边分别交于M,N两点,将![]() 以直线MN为对称轴翻折,得到
以直线MN为对称轴翻折,得到![]() .
.
设点P的纵坐标为m.
①当![]() 在
在![]() 内部时,求m的取值范围;
内部时,求m的取值范围;
②是否存在点P,使![]() ,若存在,求出满足m的值;若不存在,请说明理由.
,若存在,求出满足m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com