
【题目】如图,已知抛物线![]() 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
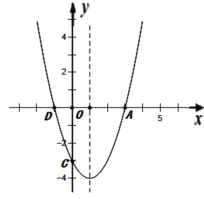
【答案】(1)A(3,0), D(-1,0), C(0,-3);(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() ,
,![]()
【解析】
由题意可知,本题考察二次函数的图像,性质与梯形.
(1)根据题意A、D、C三点,分别令横坐标和纵坐标为零,进行求解.
(2)根据题意可求出对称轴,通过△MAD的面积与△CAD的面积相等,且AD为三角形公共边,运用对称以及代入求值法进行求解.
(3)根据题意分别以BC,AP为底,运用一次方程解析式求法以及与二次函数联立方程组,进行求解
解:(1)当![]() 时,
时,![]()
解得:![]() ,
,![]()
当![]() 时,
时,![]()
∴A(3,0), D(-1,0), C(0,-3)
(2)设M点的坐标为(![]() ),可知
),可知![]() ,
,![]()
∵![]()
∴![]()
∴![]() ,即
,即![]()
∵M点在抛物线上
∴![]() ,当
,当![]() 时,
时,![]()
解得![]()
当![]() 时,
时,![]()
解得![]() 0或2
0或2
当![]() 时,点M与点C重合,故舍去;
时,点M与点C重合,故舍去;
综上所述,M点坐标![]() 或
或![]()
(3)存在;如图1所示,若![]() ,此时梯形为
,此时梯形为![]()
∵点B为点C关于抛物线对称轴的对称点
∴BC与对称轴垂直,故![]() 轴
轴
∴点![]() 位于
位于![]() 轴上,故
轴上,故![]() 点此时与D重合,对称轴为
点此时与D重合,对称轴为![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴![]() 为梯形,此时
为梯形,此时![]() 点的坐标为(-1,0)
点的坐标为(-1,0)

![]()
如图2所示,若![]() ,此时梯形为
,此时梯形为![]() ,设直线AB的解析式为:
,设直线AB的解析式为:![]()
∵直线过点A(3,0),B(2,-3)
∴![]()
解得:![]()
∴直线AB的解析式为![]()
∵![]()
∴可设直线![]() 的解析式为:
的解析式为:![]()
把C(0,-3)代入![]() ,可得n=-3
,可得n=-3
∴直线![]() 的解析式为:
的解析式为:![]()
∵![]() 为直线与抛物线的交点,可得
为直线与抛物线的交点,可得![]()
解得:![]() (舍去)或
(舍去)或![]()
![]()
将![]() 代入
代入![]() ,可得
,可得![]() ,
,
∴![]() 点的坐标为(5,12)
点的坐标为(5,12)
∴![]()
![]()
∵![]() ,
,![]()
∴![]() 为梯形
为梯形

综上所述,在抛物线上存在点P,使得以A、B、C、P四点为顶点的四边形为梯形,P点的坐标为(-1,0)或(5,12)


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
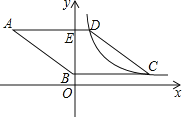
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
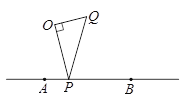
【题目】如图,点O为直线AB外一定点,点P线段AB上一动点,在直线OP右侧作Rt△OPQ,使得∠OPQ=30°,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究规律:
(1)在一组有理数![]() ,3,
,3,![]() ,
,![]() ,
,![]() 中,若其中任意两个相邻数之和都是5,则
中,若其中任意两个相邻数之和都是5,则![]() ________;
________;![]() _________;
_________;
(2)在一组有理数![]() ,
,![]() ,
,![]() ,5,
,5,![]() ,
,![]() ,
,![]() 中,若其中任意三个相邻数之和都是
中,若其中任意三个相邻数之和都是![]() ,求
,求![]() 的值;
的值;
(3)在一组有理数![]() ,
,![]() ,
,![]() ,…,
,…,![]() 中,若其中任意四个相邻数之和都是27,已知
中,若其中任意四个相邻数之和都是27,已知![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
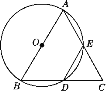
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.
(1)求证:△ABC为等边三角形.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了40名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择),请根据统计图完成下列问题:
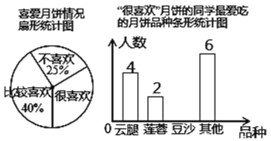
(1)被调查的40名同学中,“很喜欢”;月饼的学生有 人;条形统计图中,喜欢“豆沙”月饼的学生有 人;并补全条形统计图;
(2)若该校共有学生800人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有 人.
(3)甲同学最爱吃云腿月饼,现有重量、包装完全一样的云腿(A)、豆沙(B)、莲蓉(C)、蛋黄(D)四种月饼各一个,让甲任意选两个,请用画树状图法或列表法,求出甲选中的月饼都不是他最爱吃的云腿月饼(A)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
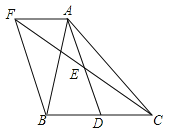
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() 是
是![]() 的中点,过
的中点,过![]() 点作
点作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)如果![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,这一天世界各地都会举办诸多与阅读有关的活动.某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
个世界读书日,这一天世界各地都会举办诸多与阅读有关的活动.某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
“读书节”活动计划书 | ||
书本类别 |
|
|
进价(单位:元) | 18 | 12 |
备注 | 用不超过16800元购进
| |
(1)陈经理查看计划书发现:![]() 类图书的标价是
类图书的标价是![]() 类图书标价的
类图书标价的![]() 倍,若顾客用
倍,若顾客用![]() 元购买图书,能单独购买
元购买图书,能单独购买![]() 类图书的数量恰好比单独购买
类图书的数量恰好比单独购买![]() 类图书的数量少
类图书的数量少![]() 本.请求出
本.请求出![]() 、
、![]() 两类图书的标价.
两类图书的标价.
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案:![]() 类图书每本按标价降价
类图书每本按标价降价![]() 元
元![]() 销售,
销售, ![]() 类图书价格不变.那么书店应如何进货才能获得最大利润?
类图书价格不变.那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:m),如果在离水面竖直距离为h(单校:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H—h).
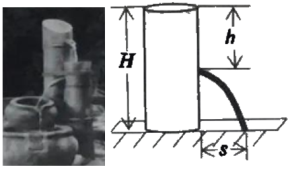
应用思考:现用高度为20cm的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连注水保证它始终盛满水,在离水面竖直距高h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16cm,求整高的高度及小孔离水面的竖直距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com