
【题目】探究规律:
(1)在一组有理数![]() ,3,
,3,![]() ,
,![]() ,
,![]() 中,若其中任意两个相邻数之和都是5,则
中,若其中任意两个相邻数之和都是5,则![]() ________;
________;![]() _________;
_________;
(2)在一组有理数![]() ,
,![]() ,
,![]() ,5,
,5,![]() ,
,![]() ,
,![]() 中,若其中任意三个相邻数之和都是
中,若其中任意三个相邻数之和都是![]() ,求
,求![]() 的值;
的值;
(3)在一组有理数![]() ,
,![]() ,
,![]() ,…,
,…,![]() 中,若其中任意四个相邻数之和都是27,已知
中,若其中任意四个相邻数之和都是27,已知![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)2,3;(2)19;(3)2.
【解析】
(1)根据在一组有理数a,3,b,c,d中,其中任意两个相邻数之和都是5,可以得到3+b=5,b+c=5,从而可以得到b、c的值;
(2)根据在一组有理数a,-9,b,5,c,d,e中,其中任意三个相邻数之和都是-6,可以得到-9+b=-9+b+5=b+5+c=5+c+d=c+d+e=-6,从而可以求得a、b、c、d、e的值,从而可以求得所求式子的值;
(3)根据在一组有理数a1,a2,a3,…,an中,其中任意四个相邻数之和都是27和a2=x-2,a77=x+5,a115=2x-6,a669=12,可以求得a1,a2,a3,a4的值,从而可以求得a2020的值.
(1)∵在一组有理数![]() ,3,
,3,![]() ,
,![]() ,
,![]() 中,其中任意两个相邻数之和都是5,
中,其中任意两个相邻数之和都是5,
∴![]() ,
,![]() ,
,
解得,![]() ,
,![]() ,
,
故答案为:2,3;
(2)∵在一组有理数![]() ,
,![]() ,
,![]() ,5,
,5,![]() ,
,![]() ,
,![]() 中,其中任意三个相邻数之和都是
中,其中任意三个相邻数之和都是![]() ,
,
∴![]() ,
,![]() ,
,
解得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
(3)∵在一组有理数![]() ,
,![]() ,
,![]() ,…,
,…,![]() 中,其中任意四个相邻数之和都是27,
中,其中任意四个相邻数之和都是27,
∴这组数是![]() ,
,![]() ,
,![]() ,
,![]() 四个数循环得到,
四个数循环得到,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ;
;
∴![]() ,
,
解得,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() 的值是2.
的值是2.


科目:初中数学 来源: 题型:
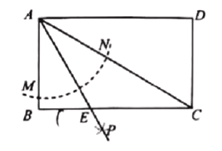
【题目】如图,矩形![]() 以点
以点![]() 为圆心,以任意长为半径作弧分别交
为圆心,以任意长为半径作弧分别交![]() 、
、![]() 于
于![]() 两点,再分别以点
两点,再分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧交于点
的长为半径作弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则矩形
,则矩形![]() 的面积等于__________.
的面积等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两直角边比为1:2的直角三角形叫做和合三角形.
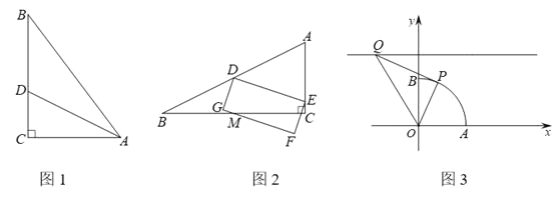
(1)如图1,△ABC中,∠C= ![]() ,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
(2)如图2,和合△ABC中,∠C= ![]() ,AC=
,AC= ![]() ,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
(3)如图3,扇形OAB中,∠AOB= ![]() ,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是
,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是 ![]() 一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有【 】

A.1组 B.2组 C.3组 D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
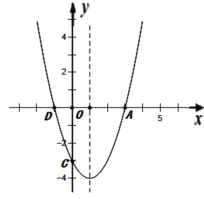
【题目】如图,已知抛物线![]() 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
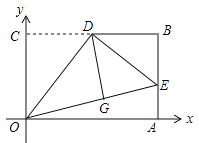
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=![]() ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com