
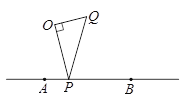
【题目】如图,点O为直线AB外一定点,点P线段AB上一动点,在直线OP右侧作Rt△OPQ,使得∠OPQ=30°,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是________.
【答案】![]()
【解析】
首先根据题意可知所有的Rt△OPQ都是相似的,从而得出点Q实质就是在一条竖直的直线上运动,据此我们假设点O在点A的正上方,且设点O(0,3),点A(0,0),点B(3,0),点P(xp,0),其中0≤xp≤3,通过待定系数法求出直线OP的解析式为:![]() ,由此得出直线OQ的解析式为:
,由此得出直线OQ的解析式为:![]() ,据此利用特殊角的三角函数值得出
,据此利用特殊角的三角函数值得出![]() ,最后在此基础上作进一步分析即可.
,最后在此基础上作进一步分析即可.
由题意得:所有的Rt△OPQ都是相似的,
∴点Q实质就是在一条竖直的直线上运动,
∴假设点O在点A的正上方,再设点O(0,3),点A(0,0),点B(3,0),点P(xp,0),其中0≤xp≤3,
∴设直线OP的解析式为:![]() ,
,
则 ,
,
∴ ,
,
∴直线OP的解析式为:![]() ,
,
∵OP⊥OQ,
∴直线OQ的解析式为:![]() ,
,
∴点Q(xQ,![]() ),
),
∴(tan30°)2=![]() ,
,
∴
∴xQ=![]() ,yQ=
,yQ=![]() ,
,
又∵0≤xp≤3,
∴3≤yQ≤3+![]() ,
,
∴点Q运动的长度为![]() ,
,
故答案为:![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,对角线AC、BD相交于点O,点E为线段BO上一点,连接CE,将CE绕点C顺时针旋转90°得到CF,连接EF交CD于点G.
(1)若AB=4,BE=![]() ,求△CEF的面积.
,求△CEF的面积.
(2)如图2,线段FE的延长线交AB于点H,过点F作FM⊥CD于点M,求证:BH+MG=![]() BE;
BE;
(3)如图3,点E为射线OD上一点,线段FE的延长线交直线CD于点G,交直线AB于点H,过点F作FM垂直直线CD于点M,请直接写出线段BH、MG、BE的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:最大公约数是指两个或多个整数共有的约数中最大的一个.我们将两个整数a、b的最大公约数表示为(a,b),如(12,18)=6;(7,9)=1.
材料二:求7x+3y=11的一组整数解,主要分为三个步骤:
第一步,用x表示y,得y![]() ;
;
第二步,找一个整数x,使得11﹣7x是3的倍数,为更容易找到这样的x,将11﹣7x变形为12﹣9x+2x﹣1=3(4﹣3x)+2x﹣1,即只需2x﹣1是3的倍数即可,为此可取x=2;
第三步,将x=2代入y![]() ,得y=﹣1.∴
,得y=﹣1.∴![]() 是原方程的一组整数解.
是原方程的一组整数解.
材料三:若关于x,y的二元一次方程ax+by=c(a,b,c均为整数)有整数解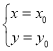 ,则它的所有整数解为
,则它的所有整数解为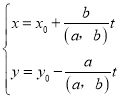 (t为整数).
(t为整数).
利用以上材料,解决下列问题:
(1)求方程(15,20)x+(4,8)y=99的一组整数解;
(2)求方程(15,20)x+(4,8)y=99有几组正整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
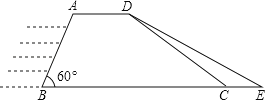
【题目】如图,马边水务部门为加强马边河防汛工作,决定对某水电站水库进行加固.原大坝的横断面是梯形ABCD,如图所示,已知迎水面AB的长为10米,∠B=60°,背水面DC的长度为10![]() 米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
(1)已知需加固的大坝长为120米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两直角边比为1:2的直角三角形叫做和合三角形.
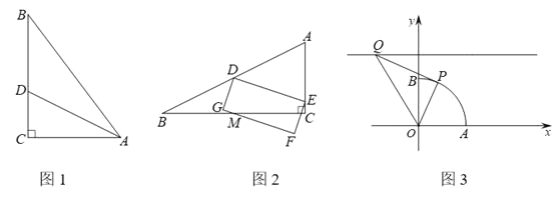
(1)如图1,△ABC中,∠C= ![]() ,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
(2)如图2,和合△ABC中,∠C= ![]() ,AC=
,AC= ![]() ,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
(3)如图3,扇形OAB中,∠AOB= ![]() ,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是
,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是 ![]() 一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
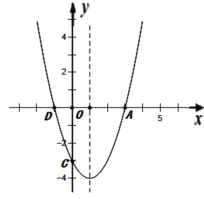
【题目】如图,已知抛物线![]() 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
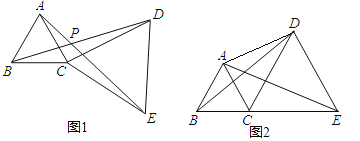
【题目】如图1,△ABC和△DCE都是等边三角形.
探究发现
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
拓展运用
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
(3)若B、C、E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为1和2,求△ACD的面积及AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com