
分析 由于已知抛物线与x轴交点坐标,则可设交点式y=a(x-1)(x+3),则设C点坐标为(0,t),利用三角形面积公式得到$\frac{1}{2}$•(1+3)|t|=6,解得t=3或t=-3,则C(0,3)或(0,-3),然后分类讨论:把C(0,3)和(0,-3)分别代入y=a(x-1)(x+3)中求出对应的a的值,从而可确定相应函数关系式.
解答 解:设抛物线的解析式为y=a(x-1)(x+3),C点坐标为(0,t),
∵△ABC的面积为6,
∴$\frac{1}{2}$•(1+3)|t|=6,解得t=3或t=-3,
∴C(0,3)或(0,-3),
当C(0,3)时,a•(-1)•3=3,解得a=-1,此时函数解析式为y=-(x-1)(x+3),即y=-x2-2x+3;
当C(0,-3)时,a•(-1)•3=-3,解得a=1,此时函数解析式为y=(x-1)(x+3),即y=x2+2x-3;
∴该二次函数的关系式为y=-x2-2x+3或y=x2+2x-3.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
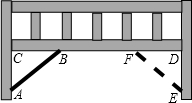 如图是一张简易木床的侧面图,现要钉上两银木条以确保其坚固耐用,木条AB已经钉上了,如果为了美观,要求木条EF与木条AB等长,那么应该怎样确定点E、F的位置?请说明理由.
如图是一张简易木床的侧面图,现要钉上两银木条以确保其坚固耐用,木条AB已经钉上了,如果为了美观,要求木条EF与木条AB等长,那么应该怎样确定点E、F的位置?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com