【题目】分解因式：x2-2xy-8y2．
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：
【题目】已知正方形ABCD，点E，F分别在射线AB，射线BC上，AE=BF，DE与AF交于点O.
（1）如图1，当点E，F分别在线段AB，BC上时，则线段DE与AF的数量关系是 ，位置关系是 .
（2）如图2，当点E在线段AB延长线上时，将线段AE沿AF进行平移至FG，连接DG.
①依题意将图2补全；
②小亮通过观察、实验提出猜想：在点E运动的过程中，始终有
.
小亮把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：连接EG，要证明
，只需证四边形FAEG是平行四边形及△DGE是等腰直角三角形.
想法2：延长AD，GF交于点H，要证明
，只需证△DGH是直角三角形.
图1 图2
请你参考上面的想法，帮助小亮证明
.（一种方法即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探究：（1）如图①，AB为⊙O的弦，点C是⊙O上的一点，在直线AB上方找一个点D，使得∠ADB=∠ACB，画出∠ADB；
（2）如图②，AB 是⊙O的弦，点C是⊙O上的一个点，在过点C的直线l上找一点P，使得∠APB<∠ACB，画出∠APB；
（3）如图③，已知足球门宽AB约为
米，一球员从距B点
米的C点（点A、B、C均在球场的底线上），沿与AC成45°的CD方向带球．试问，该球员能否在射线CD上找一点P，使得点P最佳射门点（即∠APB最大）？若能找到，求出这时点P与点C的距离；若找不到，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
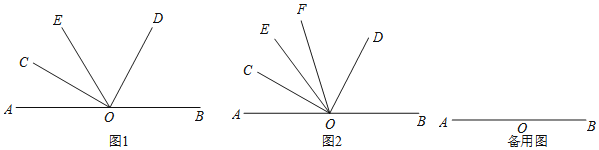
【题目】点O为直线AB上一点，在直线AB上侧任作一个∠COD，使得∠COD=90°．
（1）如图1，过点O作射线OE，当OE恰好为∠AOD的角平分线时，请直接写出∠BOD与∠COE之间的倍数关系，即∠BOD= ______ ∠COE（填一个数字）；
（2）如图2，过点O作射线OE，当OC恰好为∠AOE的角平分线时，另作射线OF，使得OF平分∠COD，求∠FOB+∠EOC的度数；
（3）在（2）的条件下，若∠EOC=3∠EOF，求∠AOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】七年级一班在召开期末总结表彰会前，班主任安排班长李小波去商店买奖品，下面是李小波与售货员的对话：
李小波：阿姨，您好！
售货员：同学，你好，想买点什么？
李小波：我只有100元，请帮我安排买10支钢笔和15本笔记本.
售货员：好，每支钢笔比每本笔记本贵2元，退你5元，请清点好，再见.
根据这段对话，你能算出钢笔和笔记本的单价各是多少吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在数轴上每相邻两点之间的距离为一个单位长度.
(1)若点A,B,C,D对应的数分别是a，b，c，d, 则可用含
的整式表示d为__________，
若3d-2a=14，则b=____________ c=_____________(填具体数值)
(2)在(1)的条件下, 点A以4个单位/秒的速度沿着数轴的正方向运动,同时点B以2个单位/秒的速度沿着数轴的正方向运动,当点A到达D点处立刻返回,与点B在数轴的
某点处相遇,求相遇点所对应的数.
(3)如果点A以2个单位/秒的速度沿着数轴的负方向运动，同时点B以4个单位/秒的
速度沿着数轴的正方向运动，是否存在某时刻使得点A与点B 到点C的距离相等，若存在请求出时间t,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
