
ЁОЬтФПЁПЕуOЮЊжБЯпABЩЯвЛЕуЃЌдкжБЯпABЩЯВрШЮзївЛИіЁЯCODЃЌЪЙЕУЁЯCOD=90ЁуЃЎ
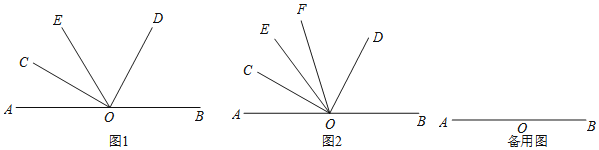
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуOзїЩфЯпOEЃЌЕБOEЧЁКУЮЊЁЯAODЕФНЧЦНЗжЯпЪБЃЌЧыжБНгаДГіЁЯBODгыЁЯCOEжЎМфЕФБЖЪ§ЙиЯЕЃЌМДЁЯBOD= ______ ЁЯCOEЃЈЬювЛИіЪ§зжЃЉЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуOзїЩфЯпOEЃЌЕБOCЧЁКУЮЊЁЯAOEЕФНЧЦНЗжЯпЪБЃЌСэзїЩфЯпOFЃЌЪЙЕУOFЦНЗжЁЯCODЃЌЧѓЁЯFOB+ЁЯEOCЕФЖШЪ§ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЁЯEOC=3ЁЯEOFЃЌЧѓЁЯAOEЕФЖШЪ§ЃЎ
ЁОД№АИЁП(1)2;(2) 135ЁуЃЛ(3)67.5Ёу.
ЁОНтЮіЁПЪдЬтЗжЮіЃК
ЃЈ1ЃЉгЩЬтвтПЩЕУЁЯAOC=90Ёу-ЁЯBODЃЛЁЯAOE=![]() ЁЯAODЃЛЁЯAOD=180Ёу-ЁЯBODЃЛАбЩЯЪіШ§ИіЙиЯЕЪНДњШыЁЯCOE=ЁЯAOE-ЁЯAOCжаЛЏМђМДПЩЕУЕНЁЯCOE=
ЁЯAODЃЛЁЯAOD=180Ёу-ЁЯBODЃЛАбЩЯЪіШ§ИіЙиЯЕЪНДњШыЁЯCOE=ЁЯAOE-ЁЯAOCжаЛЏМђМДПЩЕУЕНЁЯCOE=![]() ЁЯBODЃЌДгЖјПЩЕУГіЁЯBOD=2ЁЯCOEЃЛ
ЁЯBODЃЌДгЖјПЩЕУГіЁЯBOD=2ЁЯCOEЃЛ
ЃЈ2ЃЉгЩOCЮЊЁЯAOEЕФНЧЦНЗжЯпЃЌOFЦНЗжЁЯCODПЩЕУЃКЁЯAOC=ЁЯCOEЃЌЁЯDOF=ЁЯCOF=45ЁуЃЛНсКЯЁЯBOD+ЁЯAOC=90ЁуЃЌЁЯEOC+ЁЯFOB=ЁЯEOC+ЁЯFOD+ЁЯBODМДПЩЧѓЕУЁЯEOC+ЁЯFOBЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчБИгУЭМЃЌЩшЁЯEOF= ![]() ЃЌдђЁЯEOC=
ЃЌдђЁЯEOC=![]() ЃЌНсКЯЃЈ2ЃЉПЩЕУЁЯAOE=2ЁЯEOC=
ЃЌНсКЯЃЈ2ЃЉПЩЕУЁЯAOE=2ЁЯEOC=![]() ЃЌЁЯCOF=
ЃЌЁЯCOF=![]() =45ЁуЃЌгЩДЫМДПЩНтЕУЁЯAOE=67.5Ёу.
=45ЁуЃЌгЩДЫМДПЩНтЕУЁЯAOE=67.5Ёу.
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЁЯBOD=2ЁЯCOEЃЛРэгЩШчЯТЃК
ЁпЁЯCOD=90ЁуЃЎ
ЁрЁЯBOD+ЁЯAOC=90ЁуЃЌ
ЁпOEЦНЗжЁЯAODЃЌ
ЁрЁЯAOE=ЁЯDOE=![]() ЁЯAODЃЌ
ЁЯAODЃЌ
гжЁпЁЯBOD=180Ёу-ЁЯAODЃЌ
ЁрЁЯCOE=ЁЯAOE-ЁЯAOC=![]() ЁЯAOD-ЃЈ90Ёу-ЁЯBODЃЉ=
ЁЯAOD-ЃЈ90Ёу-ЁЯBODЃЉ=![]() ЃЈ180Ёу-ЁЯBODЃЉ-90Ёу+ЁЯBOD=
ЃЈ180Ёу-ЁЯBODЃЉ-90Ёу+ЁЯBOD=![]() ЁЯBODЃЌ
ЁЯBODЃЌ
ЁрЁЯBOD=2ЁЯCOEЃЛ
ЃЈ2ЃЉЁпOCЮЊЁЯAOEЕФНЧЦНЗжЯпЃЌOFЦНЗжЁЯCODЃЌ
ЁрЁЯAOC=ЁЯCOEЃЌЁЯCOF=ЁЯDOF=45ЁуЃЌ
ЁрЁЯFOB+ЁЯEOC=ЁЯDOF+ЁЯBOD+ЁЯAOC=45Ёу+90Ёу=135ЁуЃЛ
ЃЈ3ЃЉШчБИгУЭМЃКЁпЁЯEOC=3ЁЯEOFЃЌ
ЁрЩшЁЯEOF=xЃЌдђЁЯEOC=3xЃЌ
ЁрЁЯCOF=4xЃЌ
ЁрНсКЯЃЈ2ЃЉПЩЕУЃКЁЯAOE=2ЁЯCOE=6xЃЌЁЯCOF=4x=45ЁуЃЌ
НтЕУЃКx=11.25ЁуЃЌ
ЁрЁЯAOE=6ЁС11.25Ёу=67.5ЁуЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧвЛИіГЄЮЊ2mЁЂПэЮЊ2nЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖОљЗжГЩЫФПщаЁГЄЗНаЮЃЌШЛКѓАДЭМ2ЕФаЮзДЦДГЩвЛИіе§ЗНаЮЁЃ


ЃЈ1ЃЉФуШЯЮЊЭМ2жаЕФвѕгАВПЗжЕФе§ЗНаЮЕФБпГЄЕШгкЖрЩй?
ЃЈ2ЃЉЧыгУСНжжВЛЭЌЕФЗНЗЈЧѓЭМ2жавѕгАВПЗжЕФУцЛ§ЃК
ЗНЗЈ1ЃК ЃЛ
ЗНЗЈ2ЃК ЃЛ
ЃЈ3ЃЉЙлВьЭМ2ФуФмаДГіЯТСаШ§ИіДњЪ§ЪНжЎМфЕФЕШСПЙиЯЕТ№?
ДњЪ§ЪНЃКЃЈm+nЃЉ2ЃЌЃЈm-nЃЉ2ЃЌmnЃЎ ЃЛ
ЃЈ4ЃЉИљОнЃЈ3ЃЉЬтжаЕФЕШСПЙиЯЕЃЌНтОіШчЯТЮЪЬтЃК
Шєa+b=7ЃЌab=5ЃЌдђЃЈa-bЃЉ2== ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєНЋЕуAЃЈ1ЃЌ3ЃЉЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ4ИіЕЅЮЛЕУЕНЕуBЃЌдђЕуBЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈЉ2ЃЌЉ1ЃЉ
B.ЃЈЉ1ЃЌ0ЃЉ
C.ЃЈЉ1ЃЌЉ1ЃЉ
D.ЃЈЉ2ЃЌ0ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁЯ1=30ЁуЃЌдђЁЯ1ЕФгрНЧЖШЪ§ЃЈ ЃЉ
A.160Ёу
B.150Ёу
C.70Ёу
D.60Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСагяОфе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. ЖдНЧЯпЛЅЯрДЙжБЕФЫФБпаЮЪЧСтаЮ
B. гаСНЖдСкНЧЛЅВЙЕФЫФБпаЮЮЊЦНааЫФБпаЮ
C. ОиаЮЕФЖдНЧЯпЯрЕШ
D. ЦНааЫФБпаЮЪЧжсЖдГЦЭМаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіШёНЧЕФгрНЧМгЩЯ90ЁуЃЌОЭЕШгк( )
A.етИіШёНЧЕФгрНЧ
B.етИіШёНЧЕФВЙНЧ
C.етИіШёНЧЕФ2БЖ
D.етИіШёНЧЕФ3БЖ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com