
【题目】如图,已知A(﹣4,n),B(2,﹣4)是反比例函数y= ![]() 的图象和一次函数y=ax+b的图象的两个交点.
的图象和一次函数y=ax+b的图象的两个交点. 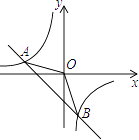
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出不等式ax+b﹣ ![]() <0的解集.
<0的解集.
【答案】
(1)解:把B(2,﹣4)代入y= ![]() 的得m=2×(﹣4)=﹣8,
的得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣ ![]() ,
,
把A(﹣4,n)代入y=﹣ ![]() 得﹣4n=﹣8,解得n=2,
得﹣4n=﹣8,解得n=2,
把A(﹣4,2)和B(2,﹣4)代入y=kx+b得 ![]() ,
,
解得 ![]() .
.
所以一次函数的解析式为y=﹣x﹣2
(2)解:直线y=﹣x﹣2与x轴交于点C(﹣2,0),
S△AOB=S△AOC+S△BOC= ![]() ×2×2+
×2×2+ ![]() ×2×4=6
×2×4=6
(3)解:不等式kx+b﹣ ![]() <0的解集为﹣4<x<0或x>2;
<0的解集为﹣4<x<0或x>2;
故答案为:﹣4<x<0或x>2.
【解析】(1)先把B(2,﹣4)代入y= ![]() 得到k=﹣8,再把A(﹣4,n)代入y=﹣
得到k=﹣8,再把A(﹣4,n)代入y=﹣ ![]() 可求出n=2,然后利用待定系数法确定一次函数的解析式;(2)先求出直线y=﹣x﹣2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;(3)观察函数图象得到当x<﹣4或0<x<2时,一次函数的图象在反比例函数图象上方,即使ax+b﹣
可求出n=2,然后利用待定系数法确定一次函数的解析式;(2)先求出直线y=﹣x﹣2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;(3)观察函数图象得到当x<﹣4或0<x<2时,一次函数的图象在反比例函数图象上方,即使ax+b﹣ ![]() <0.
<0.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上, 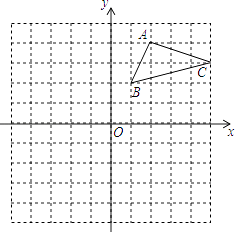
(1)画出△ABC关于x轴对称的△A1B1C1 .
(2)画出△ABC绕原点O旋转180°后的△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A是双曲线y= ![]() (x>0)上一点,过点A作AB∥y轴,交双曲线y=﹣
(x>0)上一点,过点A作AB∥y轴,交双曲线y=﹣ ![]() (x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为 .
(x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架方梯AB长25米,如图所示,斜靠在一面上:

(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是Δ
是Δ![]() 的一个外角,我们容易证明
的一个外角,我们容易证明![]() =
=![]() ,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(![]() )如图2,
)如图2,![]() 与
与![]() 分别为
分别为![]() 的两个外角,则
的两个外角,则![]()
![]() (横线上填 >、< 或=)
(横线上填 >、< 或=)
初步应用:
(![]() )如图3,在
)如图3,在![]() 纸片中剪去
纸片中剪去![]() ,得到四边形
,得到四边形![]() ,
,![]() ,则
,则![]() .
.
(![]() )解决问题:如图4,在
)解决问题:如图4,在![]() 中,
中,![]() 、
、![]() 分别平分外角
分别平分外角![]() 、
、![]() ,
,![]() 与
与![]() 有何数量关系?请利用上面的结论直接写出答案 .
有何数量关系?请利用上面的结论直接写出答案 .
(![]() )如图5,在四边形
)如图5,在四边形![]() 中,
中,![]() 、
、![]() 分别平分外角
分别平分外角![]() 、
、![]() ,请利用上面的结论探究
,请利用上面的结论探究![]() 与
与![]() 、
、![]() 的数量关系.
的数量关系.

图1 图2 图3

图4 图5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.

(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=10,EF=6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、20、100、50、10的区域,顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张。(转盘等分成20份)

(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么她获得100元以上(包括100元)券的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com