Question

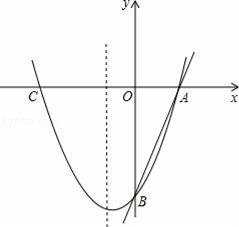
如图，已知直线y=3x﹣3分别交x轴、y轴于A、B两点，抛物线y=x²+bx+c经过A、B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．

（1）求抛物线的解析式；

（2）求△ABC的面积；

（3）在抛物线的对称轴上，是否存在点M，使△ABM为等腰三角形？若不存在，请说明理由；若存在，求出点M的坐标．

　

Answer 1

【考点】二次函数综合题．

【专题】综合题；压轴题．

【分析】（1）根据直线解析式求出点A及点B的坐标，然后将点A及点B的坐标代入抛物线解析式，可得出b、c的值，求出抛物线解析式；

（2）由（1）求得的抛物线解析式，可求出点C的坐标，继而求出AC的长度，代入三角形的面积公式即可计算；

（3）根据点M在抛物线对称轴上，可设点M的坐标为（﹣1，m），分三种情况讨论，①MA=BA，②MB=BA，③MB=MA，求出m的值后即可得出答案．

【解答】解：（1）∵直线y=3x﹣3分别交x轴、y轴于A、B两点，

∴可得A（1，0），B（0，﹣3），

把A、B两点的坐标分别代入y=x²+bx+c得：，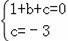

解得：．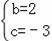

∴抛物线解析式为：y=x²+2x﹣3．

（2）令y=0得：0=x²+2x﹣3，

解得：x₁=1，x₂=﹣3，

则C点坐标为：（﹣3，0），AC=4，

故可得S_△ABC=AC×OB=×4×3=6．

（3）存在，理由如下：

抛物线的对称轴为：x=﹣1，假设存在M（﹣1，m）满足题意：

讨论：

①当MA=AB时，

∵OA=1，OB=3，

∴AB=，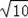

，

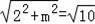
解得：，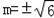

∴M₁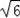（﹣1，），M₂（﹣1，﹣）；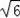

②当MB=BA时，，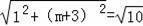

解得：M₃=0，M₄=﹣6，

∴M₃（﹣1，0），M₄（﹣1，﹣6）（不合题意舍去），

③当MB=MA时，，

解得：m=﹣1，

∴M₅（﹣1，﹣1），

答：共存在4个点M₁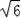（﹣1，），M₂（﹣1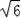，﹣），M₃（﹣1，0），M₄（﹣1，﹣1）使△ABM为等腰三角形．

【点评】本题考查了二次函数的综合题，涉及了待定系数法求二次函数解析式、等腰三角形的性质及三角形的面积，难点在第三问，注意分类讨论，不要漏解．