
【题目】阅读下列材料:
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G.使得∠EGB=∠EAB,连接AG.
求证:EG=AG+BG.
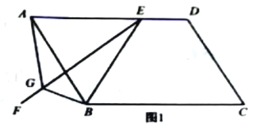
小明同学的思路是:作∠CAM=∠EAB交CE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
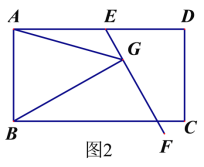
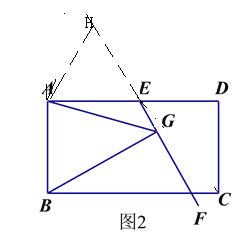
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EC、AG、BG之间的数量关系,并证明你的结论.
解:线段EG、AG、BG之间的数量关系为___________________________________________________.证明:
【答案】(1)详见解析;(2)EG+BG=![]() AG,证明详见解析.
AG,证明详见解析.
【解析】
(1)作∠GAH=∠EAB交GE于点H,证△ABG≌OAEH,再证ΔACH是等边三角形,得AG=HG ,EG=AG+BG;(2)作∠GAH=∠EAB交GE的延长线于点H,则∠GAB=∠HAE,证ΔABG≌ΔAEH,得BG=EH,AG=AH,再证ΔAGH是等腰直角三角形,可得![]() AG=HG.故EG+BG=
AG=HG.故EG+BG=![]() AG.
AG.
(1)证明:如图1,作∠GAH=∠EAB交GE于点H,
则∠GAB=∠HAE.
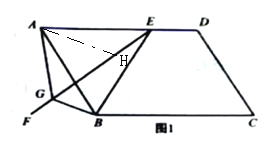
∵∠EAB=∠EGB,∠AOE=∠BOF,
∴∠ABG=∠AEH
在ΔABG和ΔAEH中
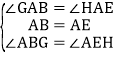
所以△ABG≌OAEH
∴BG=EH,AG=AH
∵∠GAH=∠EAB=60°
∴ΔACH是等边三角形
∴AG=HG.
∴EG=AG+BG
(2)EG+BG=![]() AG
AG
证明:
如图2,作∠GAH=∠EAB交GE的延长线于点H,则∠GAB=∠HAE
∵∠EGB=∠EAB=90°
∴∠ABG+∠AEG=∠AEG+∠AEH=180°
∴∠ABG=∠AEH.
在ΔABG和ΔAEH中
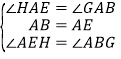
∴ΔABG≌ΔAEH
∴BG=EH,AG=AH
∵∠GAH=∠EAB=90°
ΔAGH是等腰直角三角形
∴![]() AG=HG
AG=HG
∴EG+BG=![]() AG
AG


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图1,点![]() 在线段
在线段![]() 上,图中共有三条线段
上,图中共有三条线段![]() ,
,![]() 和
和![]() ,若其中有一条线段的长度是另外一条线段长度的2倍,则称点
,若其中有一条线段的长度是另外一条线段长度的2倍,则称点![]() 是线段
是线段![]() 的“巧点”.
的“巧点”.
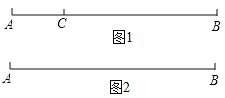
(1)线段的中点_________这条线段的“巧点”;(填“是”或“不是”);
(2)如图2,已知![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速运动;点
匀速运动;点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速运动,点
匀速运动,点![]() ,
,![]() 同时出发,当其中一点到达终点时,运动停止.设移动的时间为
同时出发,当其中一点到达终点时,运动停止.设移动的时间为![]() ,当
,当![]() _________
_________![]() 时,
时,![]() 为
为![]() 的“巧点”.
的“巧点”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:“2_3_5_9”,在每个“____”上,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若![]() ,请推算“____”上的符号;
,请推算“____”上的符号;
(3)在“2__3__5+9”的“__”上填入符号后,使计算所得数最小,直接写出填上符号后的算式及算式的计算结果的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() 为反比例函数.
为反比例函数.
(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 ;(填变化情况)
(3)求出﹣2≤x≤﹣![]() 时,y的取值范围.
时,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数按要求分类
+8.3,-4,-0.8,-![]() ,0,π,90,-|-24|,15%,
,0,π,90,-|-24|,15%,![]() 中,
中,
负数有______________________________,
分数有______________________________.
整数有______________________________.
有理数有______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上点![]() 、
、![]() 对应的数分别为
对应的数分别为![]() 、
、![]() ,且满足
,且满足![]() ,点
,点![]() 对应点的数为-3.
对应点的数为-3.
(1)![]() ______,
______,![]() ______;
______;
(2)若动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发向右运动,点
同时出发向右运动,点![]() 的速度为3个单位长度/秒;点
的速度为3个单位长度/秒;点![]() 的速度为1个单位长度/秒,求经过多长时间
的速度为1个单位长度/秒,求经过多长时间![]() 、
、![]() 两点的距离为
两点的距离为![]() ;
;
(3)在(2)的条件下,若点![]() 运动到点
运动到点![]() 立刻原速返回,到达点
立刻原速返回,到达点![]() 后停止运动,点
后停止运动,点![]() 运动至点
运动至点![]() 处又以原速返回,到达点
处又以原速返回,到达点![]() 后又折返向
后又折返向![]() 运动,当点
运动,当点![]() 停止运动点
停止运动点![]() 随之停止运动.求在整个运动过程中,两点
随之停止运动.求在整个运动过程中,两点![]() ,
,![]() 同时到达的点在数轴上表示的数.
同时到达的点在数轴上表示的数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com