
【题目】如图,![]() 为直线
为直线![]() 上一点,
上一点,![]() 平分
平分![]() ,
,![]() .
.
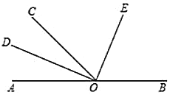
(1)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(2)猜想:![]() 是否平分
是否平分![]() ?请直接写出你猜想的结论;
?请直接写出你猜想的结论;
(3)与![]() 互余的角有:______.
互余的角有:______.
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
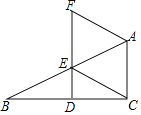
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G.使得∠EGB=∠EAB,连接AG.
求证:EG=AG+BG.
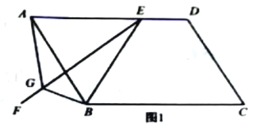
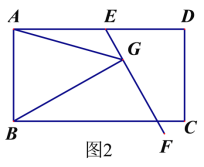
小明同学的思路是:作∠CAM=∠EAB交CE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EC、AG、BG之间的数量关系,并证明你的结论.
解:线段EG、AG、BG之间的数量关系为___________________________________________________.证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民小明上星期六买进某公司股票1000股,每股20元,下表为本周内每日该股票的涨跌情况(单位.元)
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股 涨跌 | +4 | +4.5 | -1 | -2.5 | -5 | +2 |
(1)星期四收盘时,每股是多少元?
(2)本周内每股最高价多少元?最低价多少元?
(3)已知小明买进股票时付了2%0的手续费,卖出时还需付成交额2%0的手续费和1%0的交易税,如果小明在星期六收盘前将全部股票卖出,它的收益情况如何?(注:2%0=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在一条可以折叠的数轴上,点A,B分别表示数-9和4.
(1)A,B两点之间的距离为________.
(2)如图2,如果以点C为折点,将这条数轴向右对折,此时点A落在点B的右边1个单位长度处,则点C表示的数是________.
(3)如图1,若点A以每秒3个单位长度的速度沿数轴向右运动,点B以每秒2个单位长度的速度也沿数轴向右运动,那么经过多少时间,A、B两点相距4个单位长度?
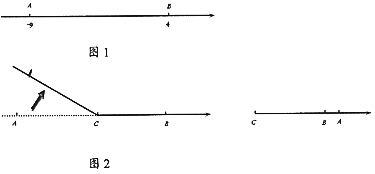
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人在一次射击比赛中击中靶的情况(击中靶中心“×”所在的圆面为10环,靶中各数字表示该数所在圆环被击中所得的环数),每人射击了6次.
(1)请用列表法将他俩的射击成绩统计出来;
(2)请你运用所学的统计知识做出分析,从两个不同角度评价甲、乙两人的打靶成绩.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C![]() 90°,AC
90°,AC![]() BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
(1)判断直线AB与⊙D的位置关系并证明.
(2)若AC![]() 1,求
1,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com