
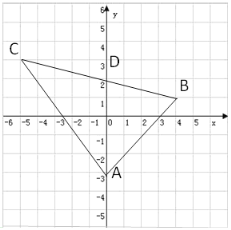
【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】小茗在一张纸上画一条数轴,并在数轴上标出![]() 、
、![]() 两个点,点
两个点,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是12.
表示的数是12.
(1)若数轴上点![]() 与点
与点![]() 相距3个单位长度,求点
相距3个单位长度,求点![]() 所表示的数;
所表示的数;
(2)将这张纸对折,使点![]() 与点
与点![]() 刚好重合,折痕与数轴交于点
刚好重合,折痕与数轴交于点![]() ,求点
,求点![]() 表示的数;
表示的数;
(3)点![]() 和点
和点![]() 同时从初始位置沿数轴向左运动,点
同时从初始位置沿数轴向左运动,点![]() 的速度是每秒1个单位长度,点
的速度是每秒1个单位长度,点![]() 的速度是每秒2个单位长度,运动时间是
的速度是每秒2个单位长度,运动时间是![]() 秒.是否存在
秒.是否存在![]() 的值,使
的值,使![]() 秒后点
秒后点![]() 到原点的距离等于点
到原点的距离等于点![]() 到原点的距离的两倍?若存在,请求出
到原点的距离的两倍?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模型介绍:古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸侧的两个军营A、B,他总是先去A营,再到河边饮马,之后再去B营,如图①,他时常想,怎么走才能使每天的路程之和最短呢?
大数学家海伦曾用轴对称的方法巧妙的解决了这问题.
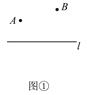
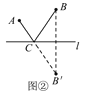
如图②,作B关于直线l的对称点B′,连接AB′与直线l交于点C,点C就是所求的位置.
请你在下列的阅读、应用的过程中,完成解答.
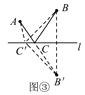
(1)理由:如图③,在直线l上另取任一点C′,连接AC′,BC′,B′C′,
∵直线l是点B,B′的对称轴,点C,C′在l上,
∴CB=_______,C′B=_______.
∴AC+CB=AC+CB′=_______.
在△AC′B′中,∵AB′<AC′+C′B′,∴AC+CB<AC′+C′B′,即AC+CB最小.
归纳小结:
本问题实际是利用轴对称变换的思想,把A、B在直线的同侧问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中C为AB′与l的交点,即A、C、B′三点共线).
本问题可拓展为“求定直线上一动点与直线外两定点的距离和的最小值”问题的数学模型.
(2)模型应用
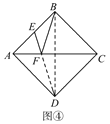
①如图 ④,正方形ABCD的边长为2,E为AB的中点,F是AC上一动点,求EF+FB的最小值.
解决这个问题,可以借助上面的模型,由正方形的对称性可知,B与D关于直线AC对称,连接ED交AC于F,则EF+FB的最小值就是线段DE的长度,EF+FB的最小值是_______.
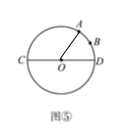
②如图⑤,已知⊙O的直径CD为4,∠AOD的度数为60°,点B是弧AD的中点,在直径CD上找一点P,使BP+AP的值最小,则BP+AP的最小值是_______;
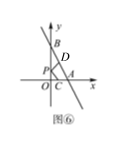
③如图⑥,一次函数y=-2x+4的图象与x,y轴分别交于A,B两点,点O为坐标原点,点C与点D分别为线段OA,AB的中点,点P为OB上一动点,求PC+PD的最小值,并写出取得最小值时P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只跳蚤在第一象限及x轴、y轴上跳动,第一秒它从原点跳动到点(0,1),第二秒它从点(0,1)跳到点(1,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],每秒跳动一个单位长度,那么30秒后跳蚤所在位置的坐标是___.
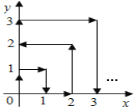
查看答案和解析>>
科目:初中数学 来源: 题型:
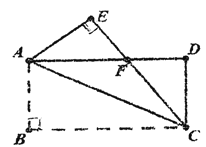
【题目】如图,AC是矩形ABCD的一条对角线,沿AC折叠使点B落在点E处。
(1)求证△AEF≌△CDF.
(2)若AB=4,BC=8,求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课本中,有这样一道题:已知:如(图1),∠B+∠C=∠BEC求证:AB∥CD
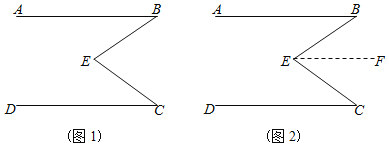
(1)请补充下面证明过程
证明:过点E,做EF∥AB,如(图2)
∴∠B=∠
∵∠B+∠C=∠BEC∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代换)
∴∠ =∠ (等式性质)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一条直线的两条直线互相平行)
(2)请再选用一种方法,加以证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春 | 出发时间 | 到站时间 | 里程(km) |
普通车 | 7:00 | 11:00 | 300 |
快车 | 7:30 | 10:30 | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com