
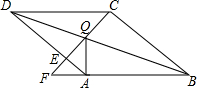
 在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.
在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.
|
| DC |
| BF |
| CQ |
| QF |
2
| ||
| 3 |
2
| ||
| 3 |
| AQ2+AB2 |
(
|
4
| ||
| 3 |


科目:初中数学 来源: 题型:
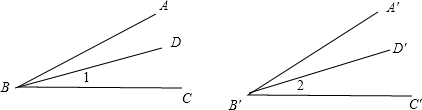
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
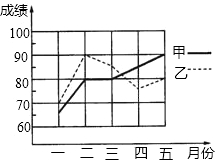 为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.
为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com