
【题目】等边△ABC的边长为6,点O是三边垂直平分线的交点,∠FOG=120°,∠FOG的两边OF,OG分别交AB,BC与点D,E,∠FOG绕点O顺时针旋转时,下列四个结论正确的是( )
①OD=OE;②![]() ;③
;③![]() ;④△BDE的周长最小值为9.
;④△BDE的周长最小值为9.
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
连接OB、OC,如图,利用等边三角形的性质得∠ABO=∠OBC=∠0CB=30°,再证明∠BOD=∠COE,于是可判断△BOD≌△COE,所以BD=CE,OD=OE,则可对①进行判断;利用![]()
![]() 得到四边形ODBE的面积
得到四边形ODBE的面积![]() ,则可对进行③判断;作OH⊥DE,如图,则DH=EH,计算出
,则可对进行③判断;作OH⊥DE,如图,则DH=EH,计算出![]() =
=![]() ,利用
,利用![]() 面积随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断;由于△BDE的周长=BC+DE=4+DE=4+
面积随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断;由于△BDE的周长=BC+DE=4+DE=4+![]() OE,根据垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.
OE,根据垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.
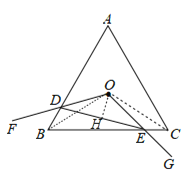
解:连接OB、OC,如图,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点0是△ABC的中心,
∴OB=OC,OB、OC分别平分∠ABC和∠ACB,
∴∠ABO=∠0BC=∠OCB=30°
∴∠BOC=120°,即∠BOE+∠COE=120°,而∠DOE=120°,即∠BOE+∠BOD=120°,
∴∠BOD=∠COE,
在△BOD和△COE中
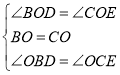
∴△BOD2≌△COE,
∴BD=CE,OD=OE,所以①正确;
∴![]() ,
,
∴四边形ODBE的面积![]() ,所以③错误;
,所以③错误;
作OH⊥DE,如图,则DH=EH,
∵∠DOE=120°,
∴∠ODE=∠OEH=30°,
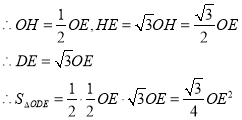
即S△ODE随OE的变化而变化,
而四边形ODBE的面积为定值,
![]() 所以②错误;
所以②错误;
∵BD=CE,
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=6+![]() OE,当OE⊥BC时,OE最小,△BDE的周长最小,此时OE=
OE,当OE⊥BC时,OE最小,△BDE的周长最小,此时OE=![]() ,
,
.△BDE周长的最小值=6+3=9,所以④正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.

(1)若AB=3,AD=![]() ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD=![]() BN .
BN .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红与小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元;且买甲种笔记本30个比买乙种笔记本20个少花10元.
(1)求甲、乙两种笔记本的单价各是多少元?
(2)若本次购进甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购进两种笔记本的总数量不少于80本,总金额不超过320元.请你设计出本次购进甲、乙两种笔记本的所有方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.![]() ∶
∶![]() C.
C.![]() ∶
∶![]() D.
D.![]() ∶
∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
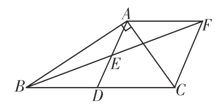
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P在线段AC上以5cm/s的速度从点A运动到点C,过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A′DP,设点P的运动时间为x(s).
(1)当点A′落在边BC上时,求x的值;
(2)在动点P从点A运动到点C过程中,当x为何值时,△A′BC是以A′B为腰的等腰三角形;
(3)如图(2),另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C,过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B′EQ,连结A′B′,当直线A′B′与△ABC的一边垂直时,求线段A′B′的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com