
【题目】如图,三角形ABC中,AC=BC,D是BC上的一点,连接AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.

【答案】(1)详见解析;(2)20°.
【解析】
(1)根据等边对等角得到∠ABC=∠BAC,由三角形外角的性质得到∠ACE=∠B+∠BAC=2∠ABC,由角平分线的定义得到∠ACE=2∠FCE,等量代换得到∠ABC=∠FCE,根据平行线的判定定理即可得到结论;
(2)根据角平分线的定义和三角形外角的性质即可得到结论.
(1)证明:∵AC=BC,
∴∠ABC=∠CAB,
∴∠ACE=∠ABC+∠CAB=2∠ABC
∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE
∴2∠ABC=2∠FCE,
∴∠ABC=∠FCE,
∴CF∥AB;
(2)∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE=∠ADC+∠DAC
∵DF平分∠ADC,
∴∠ADC=2∠FDC;
∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC,
∴2∠FCE﹣2∠FDC=∠DAC
∵∠DFC=∠FCE﹣∠FDC
∴2∠DFC=2∠FCE﹣2∠FDC=∠DAC=40°
∴∠DFC=20°.


科目:初中数学 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
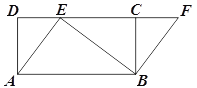
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列图形与等式的关系,并填空:
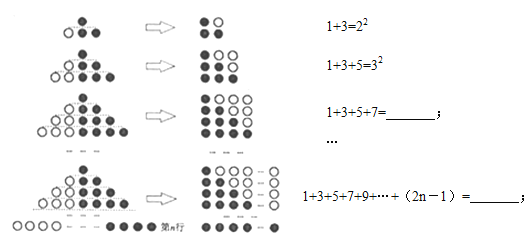
(2)利用(1)中结论,解决下列问题:
①1+3+5+…+2005= ;
②计算:101+103+105+…+199;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,
(1)求点C的坐标;
(2)连接AM,求△AMB的面积;
(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
-1、2、-4、8、-16、32、-64、……①
0、3、-3、9、-15、33、-63、……②
1、-5、7、-17、31、-65、127、……③
(1) 第①行的第8个数是___________,第①行第n个数是___________(用n的式子表示)
(2) 取第①、②、③行的第10个数分别记为a、b、c,求a-b+c的值
(3) 取每行数的第n个数,这三个数中任意两数之差的最大值为6146,则n=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.
(1)求甲、乙两厂每天各加工多少套防护服?
(2)已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元,疫情期间,某医院紧急需要3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6360元,那么甲厂至少要加工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.
(1)旋转角的大小;
(2)若AB=10,AC=8,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com