
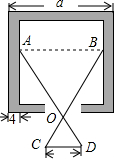
 如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).
如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示). 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
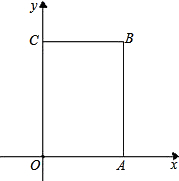 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
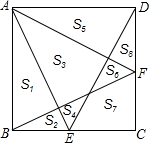 如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.
如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
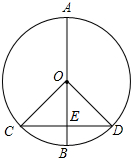 如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )| A. | ∠AOC=∠AOD | B. | BE=OE | C. | CE=DE | D. | AC=AD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.
小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com