
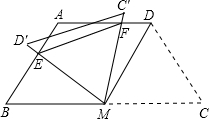
 ИзНјЈ¬өИСьМЭРОABCDЦРЈ¬ADЎОBCЈ¬AD=AB=CD=2Ј¬ЎПC=60ЎгЈ¬MКЗBCөДЦРөгЈ®
ИзНјЈ¬өИСьМЭРОABCDЦРЈ¬ADЎОBCЈ¬AD=AB=CD=2Ј¬ЎПC=60ЎгЈ¬MКЗBCөДЦРөгЈ®·ЦОц ЈЁ1Ј©Б¬ҪУBDЈ¬КЧПИЦӨГчіцЎПADB=ЎПDBCЈ¬ҪбәПМвёЙМхјюөГөҪЎПBDC=90ЎгЈ¬Ҫш¶шөГөҪDC=MDЈ¬јҙҝЙЎчMDCКЗөИұЯИэҪЗРОЈ»
ЈЁ2Ј©Б¬ҪУAMЈ¬УЙЈЁ1Ј©ЖҪРРЛДұЯРОABMDКЗБвРОЈ¬ЎчMABЈ¬ЎчMADәНЎчMCЎдDЎдКЗөИұЯИэҪЗРОЈ¬ёщҫЭASAЦӨГчЎчBMEЎХЎчAMFЈ¬УЪКЗөГөҪBE=AFЈ¬ME=MFЈ¬AE+AF=AE+BE=ABЈ¬ҪбәПЎПEMF=ЎПDMC=60ЎгЈ¬јҙҝЙЦӨГчЎчMEFКЗөИұЯИэҪЗРОЈ»
ЈЁ3Ј©№эDЧчDNЎНBCУЪNЈ¬КЧПИУЙ№ҙ№Й¶ЁАнЗуіцDNөДіӨЈ¬ЎчAEFөДЦЬіӨЧоРЎФтұЯіӨЧо¶МЈ¬MFөДЧоРЎЦөОӘөгMөҪADөДҫаАлөИУЪDNөДіӨЈ¬ҫЭҙЛЗуіцЎчAEFөДЦЬіӨЧоРЎЦөәНЎчAEFөДГж»эЧоҙуЦөЈ®
Ҫвҙр  ҪвЈәЈЁ1Ј©Б¬ҪУBDЈ¬
ҪвЈәЈЁ1Ј©Б¬ҪУBDЈ¬
ЎЯAD=ABЈ¬
ЎаЎПADB=ЎПABDЈ¬
УЦЎЯADЎОBCЈ¬
ЎаЎПADB=ЎПDBCЈ¬
ЎаЎПADB=ЎПDBCЈ¬
ЎЯФЪөИСьМЭРОABCDЦРЈ¬ЎПB=ЎПC=60ЎгЈ¬
ЎаЎПABD=ЎПDBC=30ЎгЈ¬
ЎаЎПBDC=90ЎгЈ¬
ЎаDC=MCЈ¬
ЎаЎчMDCКЗөИұЯИэҪЗРОЈ»
ЈЁ2Ј©ҪвЈәБ¬ҪУAMЈ¬ИзНј2Ј¬УЙЈЁ1Ј©ЖҪРРЛДұЯРОABMDКЗБвРОЈ¬
ЎчMABЈ¬ЎчMADәНЎчMCЎдDЎдКЗөИұЯИэҪЗРОЈ¬
ЎПBMA=ЎПBME+ЎПAME=60ЎгЈ¬ЎПEMF=ЎПAMF+ЎПAME=60ЎгЈ¬
ЎаЎПBME=ЎПAMFЈ¬
ФЪЎчBMEУлЎчAMFЦРЈ¬
$\left\{\begin{array}{l}{ЎПB=ЎПFAM}\\{BM=AM}\\{ЎПBME=ЎПAMF}\end{array}\right.$Ј¬
ЎаЎчBMEЎХЎчAMFЈЁASAЈ©Ј¬
ЎаBE=AFЈ¬ME=MFЈ¬AE+AF=AE+BE=ABЈ¬
ЎЯЎПEMF=ЎПDMC=60ЎгЈ¬
№КЎчEMFКЗөИұЯИэҪЗРОЈ»
ЈЁ3Ј©№эDЧчDNЎНBCУЪNЈ¬ИзНј2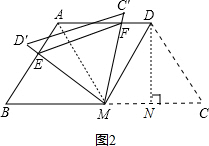
ЎЯЎПC=60ЎгЈ¬
ЎаЎПCDN=30ЎгЈ¬
ЎЯCD=2Ј¬
ЎаCN=1Ј¬
ЎаУЙ№ҙ№Й¶ЁАнөГЈәDN=$\sqrt{3}$Ј¬
ЎЯЎчEMFКЗөИұЯИэҪЗРОЈ¬
ЎаEF=MFЈ¬
ЎЯMFөДЧоРЎЦөОӘөгMөҪADөДҫаАлөИУЪDNөДіӨЈ¬јҙКЗ$\sqrt{3}$Ј¬јҙEFөДЧоРЎЦөКЗ$\sqrt{3}$Ј¬
ЎчAEFөДЦЬіӨ=AE+AF+EF=AB+EFЈ¬
ЎчAEFөДЦЬіӨөДЧоРЎЦөОӘ2+$\sqrt{3}$Ј¬
ҙЛКұЎчAEFГж»э=$\frac{1}{2}$SЖҪРРЛДұЯРОAMBN-SЎчEMFЈ¬
јҙ$\frac{1}{2}$ЎБ2ЎБ$\sqrt{3}$-$\frac{1}{2}$ЎБ$\frac{\sqrt{3}}{2}$ЎБ$\sqrt{3}$ЎБ$\sqrt{3}$=$\frac{\sqrt{3}}{4}$Ј®
ҙрЈәҙжФЪЈ¬ЎчAEFөДЦЬіӨөДЧоРЎЦөОӘ2+$\sqrt{3}$Ј¬ЎчAEFөДГж»эЧоҙуЦөОӘ$\frac{\sqrt{3}}{4}$Ј®
өгЖА ұҫМвЦчТӘҝјІйБЛјёәОұд»»өДЧЫәПМвЈ¬ҙЛМвЙжј°өҪөИұЯИэҪЗРОөДРФЦКәНЕР¶ЁЈ¬РэЧӘөДРФЦКЈ¬И«өИИэҪЗРОөДРФЦКәНЕР¶ЁЈ¬өИСьМЭРОөДРФЦКөИЦӘК¶өгЈ¬ЧЫәПФЛУГХвР©РФЦКҪшРРНЖАнКЗҪвҙЛМвөД№ШјьЈ¬ҙЛМвөЪИэОКУРТ»¶ЁөДДС¶ИЈ¬ХТіцөИұЯИэҪЗРОEMFұЯөДЧоРЎЦөөИУЪөгMөҪADөДҫаАлөИУЪDNөДіӨКЗҪвҙрұҫРЎМвөДДСөгЈ®


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | 0 | BЈ® | -$\frac{3}{2}$ | CЈ® | -$\frac{1}{3}$ | DЈ® | $\frac{1}{6}$ |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
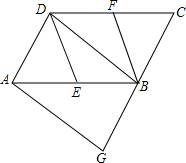 ИзНјЈ¬ФЪ?ABCDЦРЈ¬EЈ¬F·ЦұрКЗұЯABЈ¬CDөДЦРөгЈ¬BDКЗ¶ФҪЗПЯЈ¬AGЎОBDҪ»GBөДСУіӨПЯУЪөгGЈ®
ИзНјЈ¬ФЪ?ABCDЦРЈ¬EЈ¬F·ЦұрКЗұЯABЈ¬CDөДЦРөгЈ¬BDКЗ¶ФҪЗПЯЈ¬AGЎОBDҪ»GBөДСУіӨПЯУЪөгGЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
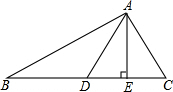 ИзНјЈ¬ФЪЎчABCЦРЈ¬ADКЗBCұЯЙПөДЦРПЯЈ¬AEЎНBCУЪEЈ¬AB=12Ј¬BC=10Ј¬AC=8Ј¬ЗуDEөДіӨЈ®
ИзНјЈ¬ФЪЎчABCЦРЈ¬ADКЗBCұЯЙПөДЦРПЯЈ¬AEЎНBCУЪEЈ¬AB=12Ј¬BC=10Ј¬AC=8Ј¬ЗуDEөДіӨЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
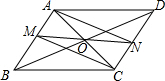 ИзНјЈ¬?ABCDөД¶ФҪЗПЯПаҪ»УЪөгOЈ¬ЦұПЯMNҫӯ№эөгOЈ¬·ЦұрРҙABЈ¬CDҪ»УЪөгMЈ¬NЈ¬Б¬ҪУANЈ¬CMЈ®ЗуЦӨЈәЛДұЯРОAMCNКЗЖҪРРЛДұЯРОЈ®
ИзНјЈ¬?ABCDөД¶ФҪЗПЯПаҪ»УЪөгOЈ¬ЦұПЯMNҫӯ№эөгOЈ¬·ЦұрРҙABЈ¬CDҪ»УЪөгMЈ¬NЈ¬Б¬ҪУANЈ¬CMЈ®ЗуЦӨЈәЛДұЯРОAMCNКЗЖҪРРЛДұЯРОЈ®Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com