
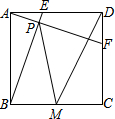
 如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为$\sqrt{10}$.
如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为$\sqrt{10}$. 分析 首先作出点D关于BC的对称点D′从而可知当点P、M、D′在一条直线上时,路径最短,当点E与点D重合,点F与点C重合时,PG和GD′均最短,即PD′最短,然后由正方形的性质和轴对称图形的性质可知:PG=1,GD′=3,最后由勾股定理即可求得PD′的长,从而可求得MD+MP的最小值.
解答 解:如图作点D关于BC的对称点D′,连接PD′,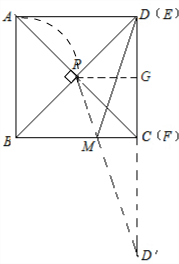
由轴对称的性质可知:MD=D′M,CD=CD′=2
∴PM+DM=PM+MD′=PD′
过点P作PE垂直DC,垂足为G,
易证AF⊥BE,故可知P的轨迹为以AB为直径的四分之一圆弧上,当点E与点D重合,点F与点C重合时,PG和GD′均最短,
∴此时,PD′最短.
∵四边形ABCD为正方形,
∴PG=$\frac{1}{2}AD=1$,GC=$\frac{1}{2}DC=1$.
∴GD′=3.
在Rt△PGD′中,由勾股定理得:PD′=$\sqrt{P{G}^{2}+GD{′}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy,直线y=x+1与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
如图,在平面直角坐标系xOy,直线y=x+1与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠ABC=∠BCD=∠CDA=90° | B. | AD=BC,AD∥BC,AC⊥BD | ||
| C. | OA=OB=OC=OD | D. | AB=CD,AD=BC,∠BAD=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )| A. | 2<x<10 | B. | 4<x<20 | C. | 8<x<12 | D. | 4<x<6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
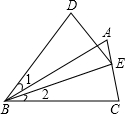 如图,AB=DB,∠1=∠2,请你添加一个适当的条件,使△ABC≌△DBE,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )
如图,AB=DB,∠1=∠2,请你添加一个适当的条件,使△ABC≌△DBE,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )| A. | BC=BE | B. | AC=DE | C. | ∠A=∠D | D. | ∠ACB=∠DEB |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com