
【题目】如图,已知A(﹣2,3)、B(4,3).C(﹣1,﹣3)

(1)点B到坐标原点的距离为 ;
(2)求BC的长;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
【答案】(1)5;(2)![]() ;(3)(0,1)或(0,5).
;(3)(0,1)或(0,5).
【解析】
(1)直接利用B点坐标和勾股定理得出点B到坐标原点的距离;
(2)利用C,B的坐标和勾股定理可得出;
(3)设点P的坐标为(0,y),根据△ABP的面积为6,A(-2,3)、B(4,3),利用数轴上的两点的距离公式和面积公式,所以![]() ,即|x-3|=2,所以x=5或x=1,即可解答.
,即|x-3|=2,所以x=5或x=1,即可解答.
解:(1)∵点B的坐标为:(4,3)
∴点B到坐标原点的距离![]() ,
,
故答案为:5;
(2)∵B(4,3).C(﹣1,﹣3)
∴![]()
(3)∵点P在y轴上,
∴设点P的坐标为(0,y)
∵△ABP的面积为6,A(-2,3)、B(4,3),
∴![]()
∴![]() ,
,
∴y=1或y=5,
∴P点的坐标为(0,1)或(0,5).


科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某中学为迎接校运会,筹集7000元购买了甲、乙两种品牌的篮球共30个,其中购买甲品牌篮球花费3000元,已知甲品牌篮球比乙品牌篮球的单价高50%,求乙品牌篮球的单价及个数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC是等边三角形,将直角三角板DEF如图放置,其中∠F=30°,让△ABC在直角三角板的边EF上向右平移(点C与点F重合时停止).

(1)如图1,当点B与点E重合时,点A恰好落在直角三角板的斜边DF上,证明:EF=2BC.
(2)在△ABC平移过程中,AB,AC分别与三角板斜边的交点为G、H,如图2,线段EB=AH是否始终成立?如果成立,请证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,EF//BC交AC、CF于M、F,若EM=3,则CE2+CF2 的值为( )

A.36B.9C.6D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.
其中正确结论的序号是( )

A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月1日起,我国将全面试行居民阶梯式电价,某市出台了实施细则,具体规定如下:
设用电量为a度,当a≤150时,电价为现行电价,每度0.51元;当150<a≤240时,在现行电价基础上,每度提高0.05元;当a>240时,在现行电价基础上,每度提高0.30元.设某户的月用电量为x(度),电费为y(元).则y与x之间的函数关系的大致图像是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距3200 m,小王、小李分别从甲、乙两地同时出发,相向而行,相遇后两人立即返回到各自出发地并停止行进.已知小李的速度始终是60 m/min,小王在相遇后以匀速返回,但比小李晚回到原地。在整个行进过程中,他们之间的距离y(m)与行进的时间t(min)之间的函数关系如图中的折线段AB—BC—CD所示,请结合图像信息解答下列问题:
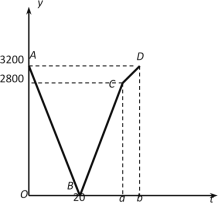
(1)小王返回时的速度= m/min,a= ,b= ;
(2)当t为何值时,小王、小李两人相距800 m?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com