Question

【题目】如图，已知∠A=∠C，∠1+∠2=180°，试猜想AB与CD之间有怎样的位置关系？并说明理由．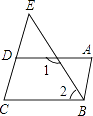

Answer 1

【答案】证明：AB∥CD，理由如下：

∵∠1+∠2=180°（已知）

∴AD∥BC（同旁内角互补，两直线平行）

∴∠EDA=∠C（两直线平行，同位角相等）

又∵∠A=∠C（已知）

∴∠A=∠EDA（等量代换）

∴AB∥CD．（内错角相等，两直线平行）

【解析】首先依据同旁内角互补，两直线平行可证明AD∥BC，然后依据平行线的性质可得到∠ADE=∠C，结合已知条件∠A=∠C，可得到∠ADE=∠A，最后，再依据内错角相等两直线平行线进行判断即可.

【考点精析】根据题目的已知条件，利用平行线的判定与性质的相关知识可以得到问题的答案，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．