【题目】如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦DE⊥AB分别交⊙O于点D、E，交AB于点H，交AC于点F．P是ED延长线上一点，且PC＝PF．

（1）求证：PC是⊙O的切线；

（2）若AD2＝DEDF，求证：CF=EF

（3）在（2）的条件下，若OH＝1，AH＝2，求线段PC的长．

参考答案：

【答案】（1）证明见解析；（2）证明见解析；（3）4．

【解析】

试题解析：（1）连接OC，证明∠OCP=90°即可．

（2）乘积的形式通常可以转化为比例的形式，通过证明三角形相似得出．

（3）可以先根据勾股定理求出DH，再通过证明△OGA≌△OHD，得出AC=2AG=2DH，求出弦AC的长．

试题解析：（1）连接OC．

∵PC=PF，OA=OC，

∴∠PCA=∠PFC，∠OCA=∠OAC，

∵∠PFC=∠AFH，DE⊥AB，

∴∠AHF=90°，

∴∠PCO=∠PCA+∠ACO=∠AFH+∠FAH=90°，

∴PC是⊙O的切线．

（2）点D在劣弧AC中点位置时，才能使AD2=DEDF，理由如下：

连接AE．

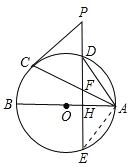
∵点D在劣弧AC中点位置，

∴∠DAF=∠DEA，

∵∠ADE=∠ADE，

∴△DAF∽△DEA，

∴AD：ED=FD：AD，

∴AD2=DEDF．

（3）连接OD交AC于G．

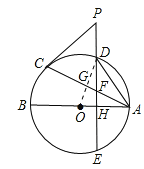
∵OH=1，AH=2，

∴OA=3，即可得OD=3，

∴DH=

∵点D在劣弧AC中点位置，

∴AC⊥DO，

∴∠OGA=∠OHD=90°，

在△OGA和△OHD中，

∴△OGA≌△OHD（AAS），

∴AG=DH，

∴AC=4．

关闭