
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
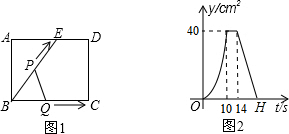
分析 根据图象可以得到BC和BE的长度,以及DE的长度,根据图2中y的值可以求得CD的长,从而可以得到AE的长,从而可以判断①;
作辅助线EF⊥BC于点F,由于EF=CD的长,从而可以得到sin∠EBC的值,可以判断②;
根据函数图象可以求得在0<t≤10时,求得△BPQ底边BQ上的高,从而可以得到△BPQ的面积,从而可以判断③;
根据题意可以分别求得在t=12时,BQ、QP、PB的长,从而判断④.
解答 解:由图象可知,
BC=BE=10,DE=14-10=4,
∴AD=10,
∴AE=AD-DE=10-4=6cm,故①正确;
作EF⊥BC于点F,作PM⊥BQ于点M,如下图所示,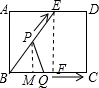
由图象可知,三角形PBQ的最大面积为40,
∴$\frac{BC•EF}{2}=\frac{10×EF}{2}=40$,
解得EF=8,
∴$sin∠EBC=\frac{EF}{BE}=\frac{8}{10}=\frac{4}{5}$,故②正确;
当0<t≤10时,△BMP∽△BFE,
∴$\frac{PM}{EF}=\frac{BP}{BE}$,即$\frac{PM}{8}=\frac{t}{10}$,
解得PM=$\frac{4t}{5}$,
∴${S}_{△BPQ}=\frac{BQ•PM}{2}=\frac{t•\frac{4t}{5}}{2}$=$\frac{2}{5}{t}^{2}$,
即$y=\frac{2}{5}{t}^{2}$,故③正确;
当t=12时,BQ=10,PQ=$\sqrt{Q{D}^{2}+D{P}^{2}}=\sqrt{{8}^{2}+{2}^{2}}=\sqrt{68}=2\sqrt{17}$,BQ=$\sqrt{A{B}^{2}+A{P}^{2}}=\sqrt{{8}^{2}+{8}^{2}}=8\sqrt{2}$,
∴△BPQ不是等腰三角形,故④错误;
故①②③正确.
故选C.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,利用数形结合的思想,找出所求问题需要的条件.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
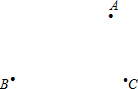 如图,已知点A,B,C,根据下列要求画图.
如图,已知点A,B,C,根据下列要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$x(2x-1)=-x2+1 | B. | (a-b+c)b=ab-b2+bc | C. | a(a-b)=a2-ab | D. | a(a2-a-1)=a3-a2-a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com