
【题目】已知,如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,△ODP是腰长为5的等腰三角形时,点P的坐标为.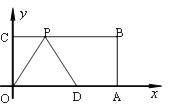
【答案】(2,4)或(3,4)或(8,4)
【解析】解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
①如图所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.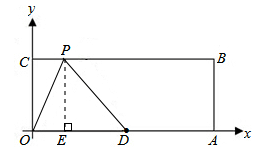
在Rt△PDE中,由勾股定理得:DE= ![]() ,
,
∴OE=OD-DE=5-3=2,
∴此时点P坐标为(2,4);
②如图所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.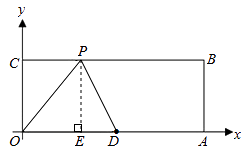
在Rt△POE中,由勾股定理得: OE= ![]() ,
,
∴此时点P坐标为(3,4);
③如图所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.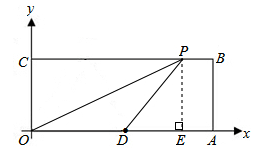
在Rt△PDE中,由勾股定理得: DE= ![]() ,
,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4).


科目:初中数学 来源: 题型:
【题目】某市火车运货站现有甲种货物1530吨,乙种货物1150 吨,安排用一列货车将这批货物运往广州,这种货车可挂A、B两种不同规格的货厢50节.已知用一节A型货厢的运费是0.5万元,用一节B型货厢的运费是0.8万元.
(1)设运输这批货物的总运费y(万元),用A型货厢的节数为x(节),试写出y与x之间的函数关系式;
(2)已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢.按此要求安排A、B两种货厢的节数,有哪几种运输方案?请你设计出来;
(3)利用函数性质说明,在这些方案中,哪种方案总运费最少?最少运费是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合采用抽样调查的是( )
A.调查18中非毕业年级学生对“社团课”的满意程度
B.调查本班同学的身高
C.为保证某种新研发的战斗机成功试飞,对其零部件进行检查
D.对乘坐高铁的乘客进行安检
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com