
分析 (1)根据题意确定出a与b的值即可;
(2)根据题意确定出a与b的值,代入计算即可求出原式的值.
解答 解:(1)由(a-2)$\sqrt{2}$+b+3=0,得到a=2,b=-3;
(2)由(2+$\sqrt{2}$)a-(1-$\sqrt{2}$)b=5整理得:(a+b)$\sqrt{2}$+(2a-b-5)=0,
∵a、b为有理数,
∴$\left\{\begin{array}{l}{a+b=0}\\{2a-b=5}\end{array}\right.$,
解得:a=$\frac{5}{3}$,b=-$\frac{5}{3}$,
则a+2b=-$\frac{5}{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
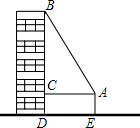 如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?
如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
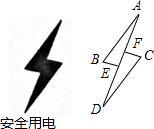 如图是一个安全用电标记图案,可以抽象为下边的几何图形,其中AB∥DC,BE∥FC,点E,F在AD上,若∠A=15°,∠B=65°,则∠AFC的度数是( )
如图是一个安全用电标记图案,可以抽象为下边的几何图形,其中AB∥DC,BE∥FC,点E,F在AD上,若∠A=15°,∠B=65°,则∠AFC的度数是( )| A. | 50° | B. | 65° | C. | 80° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
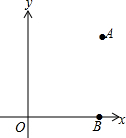 如图,在平面直角坐标系xOy中点A(6,8),点B(6,0).
如图,在平面直角坐标系xOy中点A(6,8),点B(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
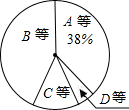 某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).| 等级 | 成绩x/分 | 频数/(人数) | 频率 |
| A | 9.0≤x≤10.0 | a | m |
| B | 7.0≤x<9.0 | 23 | 0.46 |
| C | 6.0≤x<7.0 | b | n |
| D | 0.0≤x<6.0 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
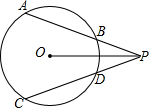 如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.
如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com