
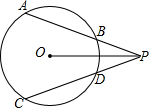
 如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.
如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.分析 (1)作OE⊥AB于E,OF⊥CD于F,连结OA、OB,根据角平分线定理得到OE=OF,再证明Rt△AOE≌Rt△COF得到AE=CF,然后证明Rt△POE≌Rt△POF,得到PE=PF,由PE-AE=PF-CF,得到PA=PC.
(2)根据垂径定理求得AE,得到PE,根据勾股定理得到OE,然后根据勾股定理求得OA.
解答 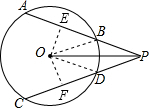 (1)证明:作OE⊥AB于E,OF⊥CD于F,连结OB、OD,如图,
(1)证明:作OE⊥AB于E,OF⊥CD于F,连结OB、OD,如图,
∵PO平分∠APC,
∴OE=OF,
在Rt△BOE和Rt△DOF中,
$\left\{\begin{array}{l}{OE=OF}\\{OB=OD}\end{array}\right.$,
∴Rt△BOE≌Rt△DOF,
∴BE=DF,
在Rt△POE和Rt△POF中,
$\left\{\begin{array}{l}{OE=OF}\\{OP=OP}\end{array}\right.$,
∴Rt△POE≌Rt△POF,
∴PE=PF,
∴PE-BE=PF-DF,
即PB=PD.
(2)解:∵AB=6,PB=1,OP=5,
∴AE=BE=3,
∴PE=4,
在Rt△POE中,OE=$\sqrt{O{P}^{2}-P{E}^{2}}$=3,
∴OA=$\sqrt{A{E}^{2}+O{E}^{2}}$=3$\sqrt{2}$.
∴⊙O的半径为3$\sqrt{2}$.
点评 本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了角平分线定理,直角三角形全等的判定方法以及勾股定理的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com