
【题目】如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD= ![]() BC.
BC. 
(1)用尺规作图的方法,过E点作EF⊥DC,垂足是点F;(不写作法,保留作图痕迹)
(2)求证:DF=CF.
【答案】
(1)解:如图,EF即为所求;
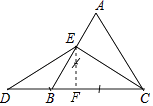
(2)证明:∵△ABC是等边三角形,点E是AB的中点,
∴CE⊥AB,BE= ![]() AB,∠ABC=60°,
AB,∠ABC=60°,
∵BD= ![]() BC,
BC,
∴BD=BE,
∴∠D=∠BED=30°.
在Rt△BCE中,
∵∠CEB=90°,∠ABC=60°,
∴∠BCE=30°,
∴DE=CE.
【解析】(1)过点E作EF⊥BC于点F即可;(2)根据等边三角形的性质得出CE⊥AB,BE= ![]() AB,再由BD=
AB,再由BD= ![]() BC可得出BD=BE,故可得出∠D=30°,在Rt△BCE中可得出∠BCE=30°,故可得出结论.
BC可得出BD=BE,故可得出∠D=30°,在Rt△BCE中可得出∠BCE=30°,故可得出结论.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某商店库存清仓,将最后两件羽绒服特价出售,甲款羽绒服卖出1200元,盈利20%,乙款羽绒服同样卖1200元,但亏损20%,该商店在这两笔交易中( )
A. 盈利100元 B. 亏损125元 C. 不赔不赚 D. 亏损100元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)(﹣2.8)+7.2+5.5+(﹣4.2)
(2)(﹣7)﹣(﹣10)+(﹣8)﹣(﹣2)
(3)![]()
(4)﹣72×2 ![]()
(5)![]()
(6)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD的长.![]()
解:∵AB=2cm,BC=2AB,
∴BC=4cm.
∴AC=AB+=cm.
∵D是AC的中点,
∴AD= ![]() =cm.
=cm.
∴BD=AD﹣=cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).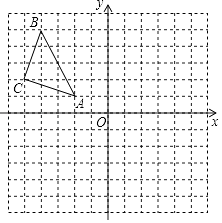
(1)画出△ABC关于y对称的△A1B1C1 , 其中,点A、B、C的对应点分别为A1、B1、C1;
(2)直接写出点A1、B1、C1的坐标; A1 , B1 , C1 .
(3)△A1B1C1的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).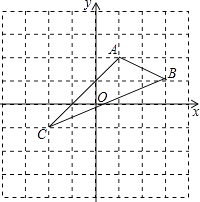
(1)在图中作出△ABC关于y轴对称的△A1B1C1 .
(2)写出A1 , B1 , C1的坐标(直接写出答案),
A1 ;B1 ;C1 .
(3)△A1B1C1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红骑车从家出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行8km到达C村,最后回到家.
(1)以家为原点,以向东方向为正方向,用1cm表示1km,画出数轴,并在数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?(直接写出答案)
(3)小红一共行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象如图所示,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是( )
的图象如图所示,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是( )

A. 没有实根 B. 有两个不等实根 C. 有两个相等实根 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
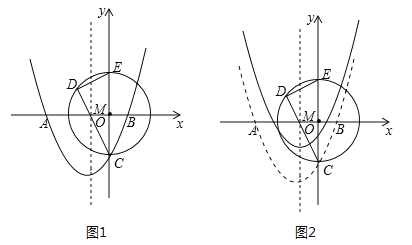
【题目】如图1,在平面直径坐标系中,抛物线![]() 与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C.
与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C.
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移![]() 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com