
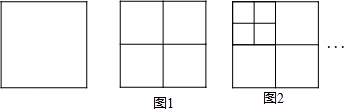
分析 (1)(1)由第一次可得5个正方形,第二次可得9个正方形,第三次可得13个正方形,可得规律:第n次可得(4n+1)个正方形;
(2)此题可看作上面几何体面积问题,即可求得答案.
解答 解:我选择第A题,
故答案为:A,
(1)∵第一次可得5个正方形,第二次可得9个正方形,第三次可得13个正方形,
∴第n次可得(4n+1)个正方形,
故答案为:4n+1;
(2)根据题意得:原式=(1-$\frac{1}{4}$)+($\frac{1}{4}$-$\frac{1}{{4}^{2}}$)+($\frac{1}{{4}^{2}}$-$\frac{1}{{4}^{3}}$)+…+($\frac{1}{{4}^{n-1}}$-$\frac{1}{{4}^{n}}$)=1-$\frac{1}{{4}^{n}}$,
故答案为:1-$\frac{1}{{4}^{n}}$.
点评 此题考查了规律问题.注意根据题意得到规律:第n次可得(4n+1)个正方形是解此题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 1500元 | B. | 1400元 | C. | 1300元 | D. | 1200元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
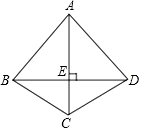 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )| A. | AC平分∠BCD | B. | AB=BD | C. | △BEC≌△DEC | D. | BC=DC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$.
如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com