
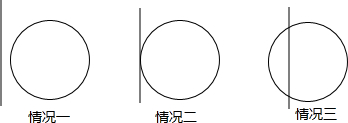
���� ���������λ���ͼ�����ۼ��ɣ�
��� ��1����Բ��������û�н���ʱ��
���ǿ���ƽ��ֳ�3���֣�
��2����Բ����������1������ʱ��
���ǿ���ƽ��ֳ�3�����֣�
��3����Բ����������2������ʱ��
���ǿ���ƽ��ֳ�4�����֣�
��4����Բ����������3������ʱ��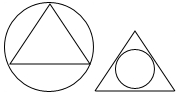
���ǿ���ƽ��ֳ�5�����֣�
��5����Բ����������4������ʱ��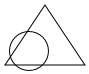
���ǿ���ƽ��ֳ�6�����֣�
��6���������κ�Բ��6������ʱ��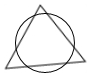
���ǿ���ƽ��ֳ�8���֣�
�������κ�Բ��6������ʱ���ֳɵ�ƽ����࣬���ֳ���8�����֣�
��������������ܰ�ƽ��ֳ�8�����֣�
�ʴ�Ϊ8��
���� ���⿼�������-ͼ�α仯��Բ��ֱ����λ�ù�ϵ��֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬�����п��������ͣ�


 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
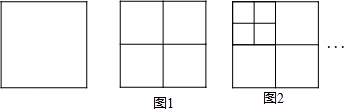
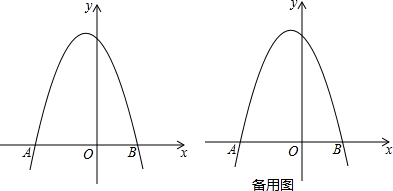
 ��ͼ��ÿ��С�����εı߳�Ϊ1��A��B��CΪС�����εĶ��㣬��֤����ABC=45�㣮
��ͼ��ÿ��С�����εı߳�Ϊ1��A��B��CΪС�����εĶ��㣬��֤����ABC=45�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
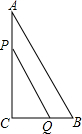 ��ͼ����ABC�У���C=90�㣬BC=5���ף�AB=5$\sqrt{5}$���ף���P�ӵ�A������AC����2����/����ٶ����յ�C�����ƶ���ͬʱ����Q�ӵ�C������CB����1����/����ٶ����յ�B�����ƶ���P��Q�����˶�����ʱ��P��Q�����ľ�����2$\sqrt{10}$���ף�
��ͼ����ABC�У���C=90�㣬BC=5���ף�AB=5$\sqrt{5}$���ף���P�ӵ�A������AC����2����/����ٶ����յ�C�����ƶ���ͬʱ����Q�ӵ�C������CB����1����/����ٶ����յ�B�����ƶ���P��Q�����˶�����ʱ��P��Q�����ľ�����2$\sqrt{10}$���ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com