
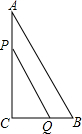
 如图,△ABC中,∠C=90°,BC=5厘米,AB=5$\sqrt{5}$厘米,点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动,同时,点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动,P、Q两点运动几秒时,P、Q两点间的距离是2$\sqrt{10}$厘米?
如图,△ABC中,∠C=90°,BC=5厘米,AB=5$\sqrt{5}$厘米,点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动,同时,点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动,P、Q两点运动几秒时,P、Q两点间的距离是2$\sqrt{10}$厘米? 分析 首先表示出PC和CQ的长,然后利用勾股定理列出有关时间t的方程求解即可.
解答 解:设P、Q两点运动x秒时,P、Q两点间的距离是2$\sqrt{10}$厘米.
在△ABC中,∠C=90°,BC=5厘米,AB=5$\sqrt{5}$厘米,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{(5\sqrt{5})^{2}-{5}^{2}}$=10(厘米),
∴AP=2x 厘米 CQ=x厘米 CP=(10-2x)厘米,
在Rt△CPQ内有PC2+CQ2=PQ2,
∴(10-2x)2+x2=(2$\sqrt{10}$)2,
整理得:x2-8x+12=0,
解得:x=2或x=6,
当x=6时 CP=10-2x=-2<0,∴x=6不合题意舍去.
∴P、Q两点运动2秒时,P、Q两点间的距离是2$\sqrt{10}$厘米.
点评 本题考查了一元二次方程的解法和应用,解决第二题的关键是设出运动时间并用运动时间表示出有关线段的长.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$.
如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{1-\sqrt{5}}}{2}$ | C. | $\frac{{1±\sqrt{5}}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com